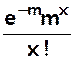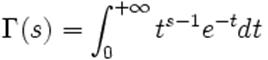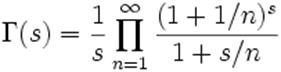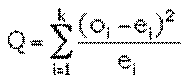LES PRINCIPALES LOIS DE PROBABILITES
Variables aléatoires
V.a. Discrète
P(X = x) = p(x)
Fonction de
répartition : F(x) = P(X < x)
V.a. Continue
La probabilité de X = x est
nulle. P(X = x) =0 (X prend une infinité de valeur)
Fonction de
répartition : F(x) = P(X
< x)
P(a ≤ X < b) = F(b) – F(a)
Densité de
probabilité : f(x)
= F’(x) Si F(X) est dérivable
f(x) = ![]() =
=![]() C’est
bien une densité de probabilité
C’est
bien une densité de probabilité
f(x) homogène
a une probabilité par unité de longueur au point considéré .
f(x) est
positif ou nul .
Si X peut prendre
toutes les valeurs de R
![]() = 1 cette intégrale est égale à P(–¥ < X < +¥) qui par définition
= 1
= 1 cette intégrale est égale à P(–¥ < X < +¥) qui par définition
= 1
Si X varie entre A et B
![]() =
1
=
1
V.a. à 2 dimensions
Discrète :
Pxy = P ( X = x et Y =y)
Distributions
marginales : Px = P(X = x) et Py
= P(Y = y)
Distributions
conditionnelles : P(X = x | Y = y
) = ![]() et
P(Y = y | X = x) =
et
P(Y = y | X = x) = ![]()
Les variables X et Y sont
indépendantes si Pxy = Px
. Py
Fonction de
répartition : F(x,y) = P(X < x et Y
< y)
Continue :
On définit la probabilité pour que (x,y)
soit dans un rectangle P(a < X <b , c < Y < d)
Si F(x,y) dérivable par rapport à x et y :
Densité de probabilité f(x,y) = 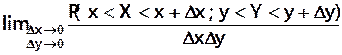
Espérance mathématique
L’espérance mathématique est
une moyenne des valeurs possibles de la V.a pondérées par leur probabilité.
V.a. discrète E(X) = å XiPi
V.a. continue E(X) = ò xf(x)dx (avec f(x) densité de probabilité)
E(X+Y) = E(X) + E(Y)
Si X et Y sont indépendantes E(XY)
= E(X)E(Y)
E(aX +b) = aE(X) + b
Variance
C’est l’espérance
mathématique du carré de l’écart à l’espérance
V(X) = E(
[ X–E(X)] 2 )
Ecart type
= ![]()
Moment d’ordre q m q = E(Xq)
å (X i )q P i
ou ò xq f(x)dx
V(X) = m2 – m12
Si X et Y indépendantes
V(X + Y) = V(X) + V(Y)
Si X et Y non
indépendantes : V(X + Y) = V(X) +V(Y) + 2Cov (X, Y)
Avec Cov
(X , Y) = E ( [ X – E(X)][Y – E(Y)] )
Moment centré d’ordre q MQ = E ( [ X – E(X) ]
q )
V(X) = M2
.
La loi Binomiale
Une série de n épreuves .
Seules possibilités réussir
(probabilité p) ou échouer (probabilité q = 1 – p)
Variable
aléatoire discrète : en général nombre de succès ou d’échecs.
Une telle série d’épreuves
obéit à la loi B(n,p)
Loi binomiale à n épreuves
dont le succès a la probabilité p.
Exemples :
Urne de Bernouilli
avec p boules blanches et q boules noires. n tirages
avec remise.
Probabilité de tirer X
blanches. On décide par exemple succès = boule blanche. Probabilité p / (p+q).
n naissances dans une famille. Garçon ou fille ont la
probabilité ½ .
Probabilité de mettre au
monde X filles. On décide succès = fille.
n mises sur la couleur rouge à la roulette.
Probabilité de gagner X fois.
Succès = la couleur rouge sort . La probabilité de rouge est 18/37.
Variable de Bernouilli X
X = 1 si succès probabilité p
X = 0 si échec probabilité q = 1 – p
E(X) = p
V(X) = p – p2 = p(1–p) = pq
La variable binomiale X (qui indique le nombre de succès) est une somme de
variables de Bernouilli.
Il suffit d’appeler X1 , X2 , ……Xn la variable de Bernouilli liée au résultat de chacune des n épreuve.
Le nombre X de succès sur n
épreuves est X = X1+…..+Xn.
Le résultat d’une série de n
épreuves peut être présenté sous la forme (X1 , X2
, ……. ;Xn)
Par exemple pour n = 7 (1101001)
qui donne pour cette série X = 4 ( 4 fois 1 et 3 fois 0)
Chaque série de résultats d’épreuves est un n–uplet de { 0 ; 1 }n
tel que (1, 1 , 0 , 1 , 0, 0 , 1).
Ωn est l’ensemble des séries
de résultats de n épreuves
il comporte 2 X 2 X 2 x …x 2 = 2n
séries possibles.
L’évènement X = x est l’ensemble des séries
qui comportent x fois le chiffre 1 et n–x fois le chiffre 0.
Le
nombre des séries de résultats pour lesquelles X = x
C’est ![]() (combinaisons
de n rangs x par x)
(combinaisons
de n rangs x par x)
Par exemple pour 7 épreuves
et X = 4 si l’on doit dénombrer
toutes les façons de situer les quatre 1 à des rangs différents dans (1, 1 , 0
, 1 , 0, 0 , 1) on va trouver ![]() .
.
La
probabilité d’une série de résultats pour laquelle X = x
La probabilité d’une
série comportant x succès (probabilité p) et n–x échecs
probabilité (q = 1– p) est
pxqn–x
(il suffit de la considérer comme l’intersection de n évènements
indépendants dont x ont la probabilité p et n – x la
probabilité q ).
Par exemple pour (1, 1 , 0 , 1 , 0, 0 , 1) est aussi la conjonction
suivante :
(1 à la 1ere épreuve) ET (1 à
la 2e) ET (0 à la 3e) ET ….ET (1
à la 7e )
Probabilité ppqpqqp = p4q3.
Donc la probabilité de X = x dans une série de n épreuves est
P(X = x) = ![]() pxqn–x
pxqn–x
Produit du nombre de
résultats favorables par la probabilité de chacun d’eux.
Par exemple pour 4 épreuves à
pile ou face (p = q = ½) on peut calculer la probabilité pour que X (nombre de
piles) prenne toutes les valeurs possibles :
|
Valeurs de X |
0 |
1 |
2 |
3 |
4 |
|
Probabilité |
|
|
|
|
|
Fonction de répartition
P(X < x) = 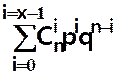
Caractéristiques
On observe X est le nombre de
tirages ayant donné lieu au même type d’évènements.
X = å Xi (somme de n variables de Bernouilli)
avec E(Xi) = p et V(Xi) = pq donc
E(X) = np
V(X) = npq
s = ![]()
Loi des fréquences :
On observe X / n la fréquence
d’un type d’évènement.
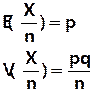
Quelques exemples
pour n = 5 (X varie de 0 à 5) , p variant de 0,1
(en bleu) à 0,5 (en vert)
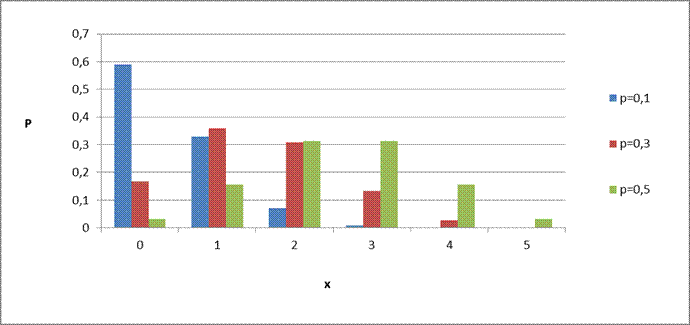
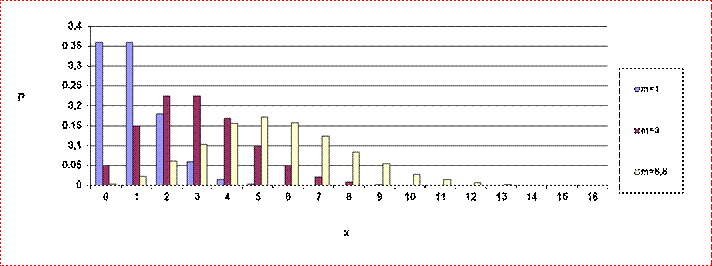
Seule la loi B(5 ; 0,5) est symétrique le maximum de
probabilité correspondant à X = 2 ou 3 .
Plus p diminue, plus le
maximum de probabilité évolue vers les petites valeurs de X et plus la
probabilité des grandes valeurs de X tend à devenir nulle rapidement.
C’est normal car les succès
sont de moins en moins probables.
La loi hypergéométrique
Série de n épreuves avec pour seule alternative le succès ou
l’échec (comme pour la loi binomiale)
MAIS : la probabilité du
succès p(r) varie avec le rang r de l’épreuve.
Variable aléatoire
discrète : en général nombre de succès ou d’échecs.
Exemple type : les tirages sans remise encore appelés tirages
exhaustifs dans une population d’effectif N .
(On ne remet pas la boule tirée dans l’urne après tirage)
On peut considérer que les
paramètres de la loi hypergéométriques sont
N l’effectif initial
F l’effectif initial favorable à la réussite
n le nombre
de tirages
Et on parle de loi H(N , F, n)
On utilise la même variable aléatoire X que pour
la loi binomiale.
Par exemple X = nombre
de boules noires tirées après n tirages dans une urne qui contient
initialement F noires et N –F blanches.
Le dénombrement des séries de résultat pour
lesquelles X = x est le même ![]()
Je numérote les épreuves par
leur rang 1, 2 , .....n et je choisis parmi ces n
rangs un ensemble de x rangs qui auront donné lieu à la réussite.
Combien de possibilités de choix ? ![]() .
.
Toutes les séries donnant X = x ont la même
probabilité Px mais celle-ci doit être évaluée une fois
P(X = x) =
![]() Px
Px
Exemple
Une urne contient 5 boules
noires et 10 boules rouges (en tout 15 boules) .
5 tirages (n = 5) . Probabilité de 3 noires (X = 3) ?
Probabilité de 11010 = ![]()
1er tirage il y a
5 boules noires sur 15
2e tirage il reste
4 boules noires sur 14
3e tirage il y a
10 boules rouges sur 13
4e tirage il reste
3 boules noires sur 12
5e tirage il reste
9 boules rouges sur 11.
Probabilité de 00111 = ![]() =
Probabilité de 11010
=
Probabilité de 11010
Pourquoi cette probabilité ne
change – t – elle pas ?
Parce que les dénominateurs
rendent compte de la diminution du nombre de boules dans l’urne qui va toujours
passer de 15 à 11 au cours de 5 tirages. Quant aux numérateurs, ils
rendent compte de l’évolution du nombre de boules de chaque couleur. Ces
nombres vont forcément évoluer de la même façon même si ce n’est pas au même
moment et donc d’un numérateur à l’autre on a seulement permuté des facteurs
semblables.
Dans ce cas, la probabilité
de X = 3 est donc ![]() .
.
![]()
Raisonnons autrement :
Il revient au même de tirer
les n boules une par une ou de tirer n boules et de compter parmi
elles les boules noires.
Parmi les N boules,
combien de séries différentes de n puis je tirer ? 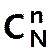 Cas
possibles équiprobables.
Cas
possibles équiprobables.
Parmi les F noires
combien de séries de x noires puis je tirer ? 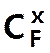
Pour chaque série de x noires,
combien de séries de n – x blanches parmi
N – F ? ![]()
Donc parmi les cas possibles,
combien sont formés de x noires et
n-x
blanches ? ![]()
![]()
On peut donc dire que
P( X = x) = 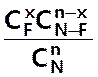
Caractéristiques :
E(X) = np (comme pour la loi binomiale)
V(X) =
npq 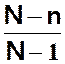 (N
effectif total avant tirage et n nombre d’épreuves)
(N
effectif total avant tirage et n nombre d’épreuves)
|
De la loi Hypergéométrique à la loi binomiale. Si N très grand
devant n et si p moyen, pas trop voisin de 0 ou 1 :
On peut faire une approximation de la loi hypergéométrique par la loi
binomiale. n < N / 10 ,
p=X/N |
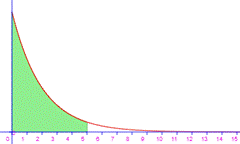
Loi exponentielle
Supposons
qu'un objet à une durée de vie sans
vieillissement.
Si on
interprète X comme la durée de vie d’un appareil, cette propriété est synonyme
de l'égalité :
PX⩾t (X⩾h+t)=P (X⩾t) qui signifie que la probabilité que l’appareil fonctionne
encore au-delà du temps h+t sachant qu’il fonctionne encore à l’instant h est
égale à la probabilité que l’appareil fonctionne au-delà du temps t .
Autrement
dit d'après les probabilités composées P(X⩾h+t)=P(x>h).P (X⩾t)
Si on
appelle F(t) est la probabilité que l'objet ait une durée de vie supérieure à t
F(h+t) =
F(h) . F(t) autrement dit
![]() ce qui est caractéristique d'une fonction exponentielle
F(t)=ekt
ce qui est caractéristique d'une fonction exponentielle
F(t)=ekt
Avec k négatif puisque
la probabilité est inférieure à 1. On pose k = –λ.
On en déduit que
 Fonction de répartition
Fonction de répartition
![]() = 1 – e–λx
= 1 – e–λx
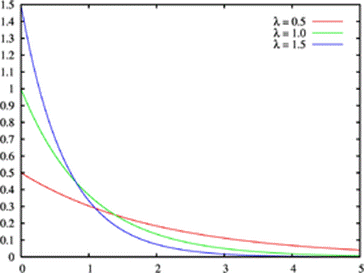
Espérance
E(x) = ![]()
Variance V(x) = ![]()
Écart type σ(x) = ![]()
Médiane (t
tel que P(x>t) = 0,5 ) ![]()
La densité
de probabilité est la dérivée par rapport à t de la fonction de répartition.
 Densité de probabilité :
Densité de probabilité :
F(x) =
λe–λt
Primitive
–e–λt
Intégrale
de 0 à ∞
![]() = 1
= 1
C'est bien une densité
de probabilité.
|
|
|
|
|
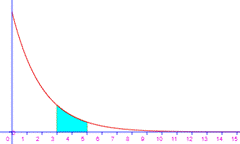
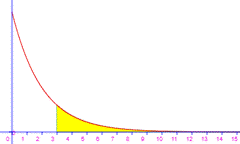
Pr(X entre
3 et 5) |
Pr(x<5)
|
Pr(x>3) |
Loi de Poisson
Processus de Poisson
Apparition
d’évènements aléatoires dans le temps ou dans l’espace.
La probabilité de réalisation d’un évènement E au cours d’une
petite période de temps Δt ou sur une petite portion d’espace ΔL ,
ΔS , ΔV que nous appellerons Δz est proportionnel à
Δz .
P(E)=
pΔz
La probabilité d’apparition de deux évènements sur Δz très petit est
négligeable
Appels
téléphoniques dans un central, pannes de machines, arrivées à un péage,
particules observées avec un appareil, points répartis au hasard sur une
droite, captation de rayon cosmiques.
Variable discrète X = nombre d’évènements observés sur Z
(temps ou espace)
P(X = x) = 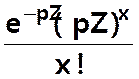 ou
ou
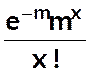 si
l’on pose m = pZ
si
l’on pose m = pZ
Des tables
donnent la valeur de P(X = x) selon la valeur de x pour différents valeurs de m
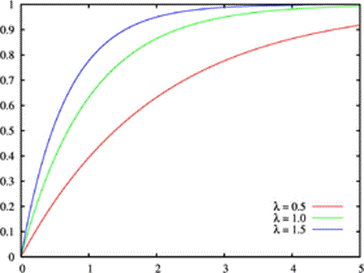
En voici 3
exemples. (m = 1 en bleu m= 3 en rouge, m=5,5 en jaune).
La loi de poisson comme limite d’une loi
binomiale
Prenons une
loi binomiale B(n, p) avec p petit (évènement rare) et n
grand (épreuves très nombreuses).
Faisons en
sorte que np soit de l’ordre de quelques unités (3 ou 4)
E(X) = np donc au cours des n épreuves,
l’évènement espéré se produira en moyenne 3 ou 4 fois.
Si l’on
imagine la succession rapide des épreuves pendant un laps de temps relativement
court , l’observateur retrouve à peu prés les conditions d’un processus de
poisson de paramètre m = np.
A partir de
B(n,p) on a
P(X=x) = 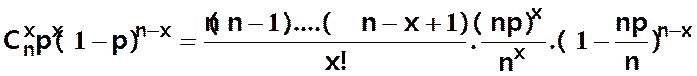
P(X=x) = 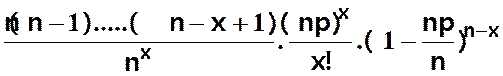
Si n è +¥ et p è 0 de telle sorte que np è m alors P(X = x) è 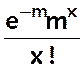
On procède à
partir de
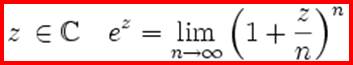
à la limite 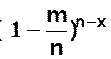 est
équivalent à
est
équivalent à 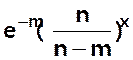
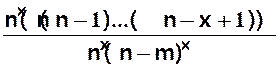 =
=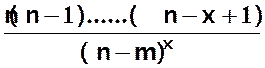 qui
se comporte comme
qui
se comporte comme![]()
(limite 1
quand nè+¥)
|
De la loi binomiale à la loi de poisson On a donc bien à la limite
la loi binomiale P(X = x) è la loi de
poisson On considère que c’est le
cas dés que n > 50 et np < 5
|
Caractéristiques de la loi de Poisson
E(X) = 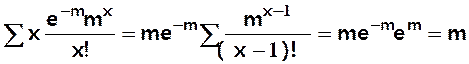 (on
reconnaît le D.L de em)
(on
reconnaît le D.L de em)
E(X) = m
V(X) = m
Loi normale
Loi normale, loi de Laplace – Gauss , loi de
Gauss.
C’est la loi
suivie par une variable aléatoire continue dont la moyenne (l’espérance
mathématique) et la médiane coïncident avec la valeur
la plus probable (le mode).
De plus
les écarts à la moyenne doivent être symétriques par rapport
à cette dernière et la probabilité de X doit diminuer de façon
significative quand on s’écarte de la moyenne, puisque, si s est l’écart type et M l’espérance
mathématique, la probabilité pour que X soit compris entre M-2s et M+2s doit être de l’ordre de 95%.
Caractéristiques de la loi normale
Dans ce qui suit
le signe ò représente une intégration sur R :
Densité de probabilité
f(x) = 
En posant  la
loi devient f(T) =
la
loi devient f(T) = 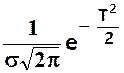
Or nous
savons que la fonction f (T) =  a
une intégrale ò f (T) dT = 1 (Gauss).
a
une intégrale ò f (T) dT = 1 (Gauss).
Donc la
fonction f peut être considérée
comme une densité de probabilité.
Alors, il en
va de même de la fonction f(X) car après changement de variable on a
ò f(x)dx = ò  = ò f (T) dT
= ò f (T) dT
D’ailleurs,
on a f(x) = f (x) si l’on
prend s = 1 et m =
0 .
La loi f (x) est appelée loi normale, centrée,
réduite et notée N(0,1)
Normale (N (0,1) ) parce que sa densité de probabilité est
de type f(x)
Centrée parce que lorsque m = 0
(N(0,1)) le graphe de la loi est
symétrique par rapport à l’axe des y
Réduite parce que le choix de s = 1 (N(0,1)) et de m = 0 a simplifié son expression.
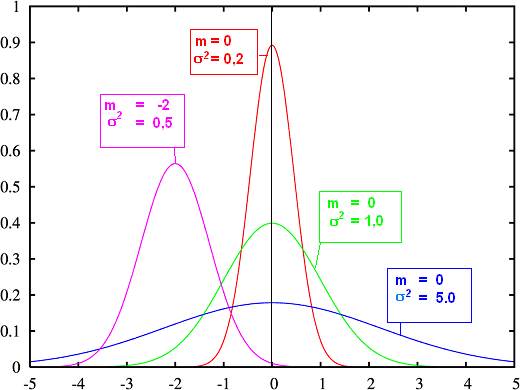
Voici le
graphe de la loi N(0,1) en vert
accompagné d’autres graphes de lois normales, centrées ( m = 0) ou non
(m=–2).
On voit que m
fixe l’emplacement du maximum de la distribution tandis que s module la dispersion des valeurs
autour de la moyenne.
Plus s est petit plus la courbe est effilée vers le
haut et la population concentrée autour de la moyenne. Plus s est grand et plus la courbe est évasée et aplatie. .
Espérance mathématique de N(m , s ) = m
Médiane de N(m , s ) = m
Mode de N(m , s ) = m (valeur la plus
fréquente)
Ecart type de N(m , s ) = s
Les tables de la loi normale
Comme le montre
le dessin ci-dessous, les répartitions gaussiennes sont telles que
P(m –0,66s < x < m + 0,66s ) » 50% ce qui veut dire qu’on trouve 50% de
l’aire située sous la courbe et au dessus de l’axe des x entre les droites
d’équation x = m – (2/3)s et x
= m + (2/3)s
P(m – 2s < x < m + 2s ) » 95% Ce qui veut dire que pour 95% de la
population le caractère X se trouve entre ces deux valeurs.
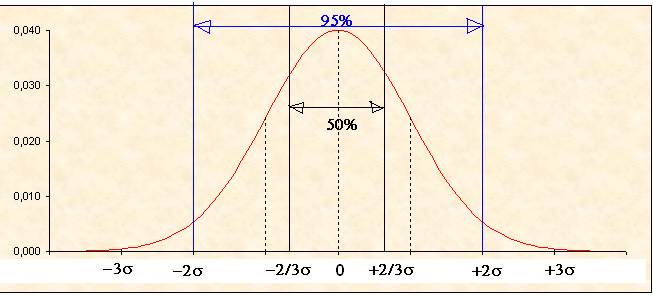
Des tables
donnent P(m – q < x < m + q )
en fonction de q
pour une loi N(m , s )
Bien sûr P(
X ≤ m – q ou X ≥ m + q ) = 1 – P(m – q < x < m + q )
Il existe
aussi une table de fonction de répartition P(T < t) = 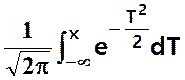 en
fonction de t
en
fonction de t
Et il ne
faut pas oublier le cas échéant le changement de variable  si
l’on nous demande P(X<x)
si
l’on nous demande P(X<x)
Approximation d’une loi binomiale B(n,p) par
une loi normale
Cette
approximation est d’autant plus judicieuse que le nombre d’épreuves n
est grand et que la probabilité p n’est pas trop éloignée de ½.
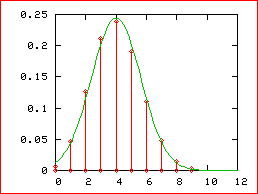 sur ce dessin
sur ce dessin
En rouge le
diagramme en bâtons de la loi B(12, 1/3)
On calcule
que :
m = np =
4 , V = npq = 8/3
Et en vert
la courbe de la loi N(4, 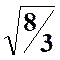 )
)
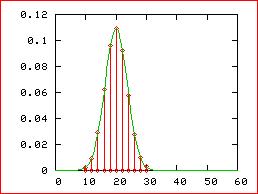
sur ce
dessin
En rouge le
diagramme en bâtons de la loi B(60, 1/3)
On calcule
que :
m = np =
20 , V = npq = 40/3
Et en vert la
courbe de la loi N(20, ![]() )
)
|
De la loi binomiale à la loi normale On considère que
l’ajustement des deux lois est convenable lorsque n, p ,
q de la loi binomiale sont tels que npq
> 10 |
Somme de variables aléatoires normales
Soit la
famille de v.a. gaussiennes : { X i de moyenne m
i et de variance V i }
Alors, la
variable Σ X i est gaussienne de moyenne Σ
m i et de variance Σ V i
Lois dérivées de la loi normale
Loi Log – normale
|
Définition : Une variable aléatoire X à valeurs dans ] 0 , + ¥ [ suit la loi Log - normale de paramètres N(m,s) si Y=log X suit la loi N(m,s) . |
De f(y)
= 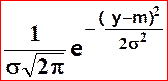
On déduit la
densité de X après changement de variable Y = Log X :
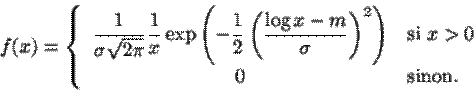
X admet
alors une espérance et une variance
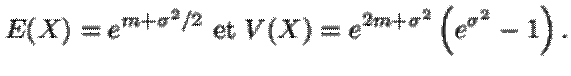
Courbe
représentative de la densité :
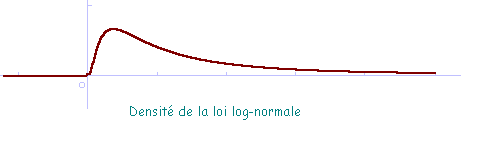
Ex : le nombre de mots dans une phrase
suit approximativement une loi log - normale.
La loi du
c2 de Pearson (lire Khi carré) et la loi de
Student sont des lois dérivées de la loi normale qui vont
faire l’objet d’une étude particulière.
La loi du c2 de Pearson
La loi du χ² (prononcer khi-deux ou khi
carré) est une loi à densité de probabilité. Cette loi est caractérisée par
un paramètre dit degrés de liberté à valeur dans l'ensemble des entiers
naturels (non nuls).
Soit ![]() n variables aléatoires indépendantes de même loi
normale centrée et réduite, alors par définition la variable X, telle que
n variables aléatoires indépendantes de même loi
normale centrée et réduite, alors par définition la variable X, telle que
![]() (X est souvent appelée χ² )
(X est souvent appelée χ² )
suit une loi du khi-2 à n degrés de liberté.
Soit ![]() une
variable aléatoire suivant une loi du χ² à
une
variable aléatoire suivant une loi du χ² à ![]() degrés
de liberté, on notera
degrés
de liberté, on notera ![]() la
loi de
la
loi de ![]() .
.
Alors la densité de ![]() notée
notée
![]() sera:
sera:
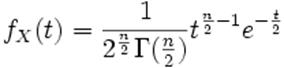 pour tout t positif
pour tout t positif
où Γ est la fonction Gamma d'Euler.
|
En
mathématiques, la fonction gamma est définie dans le demi-plan complexe
de partie réelle strictement positive par l'intégrale suivante:
|
L'espérance
mathématique de X vaut n
sa variance vaut 2n
Tables : il existe des tables donnant p(X
> x) selon la valeur de n .
|
De la loi du c2 à la loi normale : Lorsque n > 30 on
admet que si X suit une loi du c2 alors suit une loi
normale centrée réduite |
.
La somme des
carrés de m variables aléatoires normales liées par p relations
suit une loi du c2 à
n =
m – p degrés de
libertés.
Test du c2
On utilise
ce test pour juger
De l’adéquation d’une population à une distribution type (exemple loi de
poisson)
De l’homogénéité de 2 populations soupçonnées de suivre une même loi
De l’indépendance de deux populations
|
Méthode On répartit les valeurs de
l'échantillon (de taille n) dans k classes distinctes et on calcule
les effectifs de ces classes. Si l’on regroupe certaines classes pour les
doter d’un effectif plus important, k diminue en conséquence. On calcule La statistique Q donne
une mesure de l'écart existant entre les effectifs théoriques attendus et
ceux observés dans l'échantillon. En effet, plus Q sera grand, plus le
désaccord sera important. La coïncidence sera parfaite si Q=0. Le degré de
liberté (d) de la variable soumise
au test (oi) est obtenu en
soustrayant à k le nombre de relations entre les valeurs
observées qui ont été utilisées dans le paramétrage de la loi de référence. Par exemple si on a une
relation de type Σ oi = n
(loi B(n,p)) le degré de liberté devient k
– 1 Si, de plus on a eu besoin
de calculer la moyenne m des oi
pour tester l’adéquation à la loi B(n,p) (p déduit de m) ou P(m) (m paramètre de la
loi de Poisson) le degré de liberté deviendra k – 2. La table donne, pour d
degrés de libertés, une fonction de répartition de Q : la
probabilité pour que Q soit plus grand qu’une valeur donnée q. En situant Q dans
l’échelle des valeurs de q on sait que Q a entre x% et y% de chances
d’être dépassé. Plus la probabilité de Q d’être dépassé est grande,
plus l’adéquation de la loi à la série est judicieuse |
|
|
||||||||||||||||||||||||
|
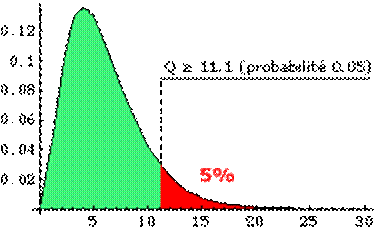
Exemple On a lancé un dé 90 fois et on a obtenu les
issues 1 à 6 (k=6) avec les effectifs suivants: 12, 16, 20, 11, 13, 18. Si le
dé n'est pas pipé (notre
Pour k-1=5 degrés de liberté
on trouve dans la table Q entre les valeurs
Ce qui signifie que la
probabilité pour Q d’être dépassé est un peu supérieure à 50% . L’adéquation de la loi à la série n’est pas fameuse.
Mais il faudrait que Q soit supérieur à 11.07 pour qu'elle soit mauvaise au
risque de 5%. Variations Dans ce cas, on connait l'effectif théorique de chaque
classe qui en fonction des probabilités (1/6)
doit être 15 occurrences d'une face de dé sur 90 lancers. 15 est l'hypothèse
"adéquation à la loi de probabilité" (effectif théorique ei). Dans d'autres cas, il
faudra juger par exemple l'adéquation
d'un échantillon de données à une loi de poisson et après avoir calculé la moyenne m de la variable
aléatoire X sur l'échantillon observé,
il faudra utiliser la loi de poisson pour calculer un effectif théorique qui
devrait être selon la valeur de X, m. P(X=x)= m Et l'utilisation de m implique que le degré de liberté de la table obtenue
diminue d'une unité. Enfin, on peut nous
demander de tester la
dépendance de 2 variables, par
exemple la dépendance d'une variable qualitative pouvant prendre trois états
(intention de vote = oui, non abstention) par rapport à 3 classes d'une
population (par exemple 18-25 ans, 26-50 ans, plus de 50 ans). Les résultats sont
présentés dans un tableau de ce type
Nos données sont les
effectifs nij
(Tableau 3 X 3 généralement LXC) Le degré de liberté est
(L-1) x (C-1) ici (3–1) x (3 – 1) = 4.
La dernière ligne et la
dernière colonne ont été rajoutées pour calculer les données théoriques de
l'hypothèse d'indépendance. En effet si la classe est indépendante de la
population au lieu de n11 il devrait y avoir une proportion de N1
fonction de la fréquence de la population 1. Soit e11 =N1 Ensuite pour chaque case du
tableau on calcule Idéalement, si la nature de
la population n'influence pas la classe, (hypothèse d'indépendance) q devrait
être nul. Si
q est petit, cela signifie que
l'effectif d'une classe est dispatché entre les 3 populations pratiquement en
fonction de leur fréquence ce qui est normal quand la nature de la population
n'influence pas la relation à une classe (population et classe sont indépendantes). Si
q est grand cela signifie que la nature
de la population influence sa relation à une ou plusieurs classes (autrement dit, il existe une forte
affinité entre certaines populations et certaines classes) puisqu'il y a un écart important par
rapport à l'indépendance. Tout le problème est de
savoir à partir de quel seuil de grandeur de q on peut considérer que la
dépendance a de grandes chances d'être effective. C'est à ce stade qu'on a
recours aux tables qui sont elles-mêmes fonction du degré de liberté..
|
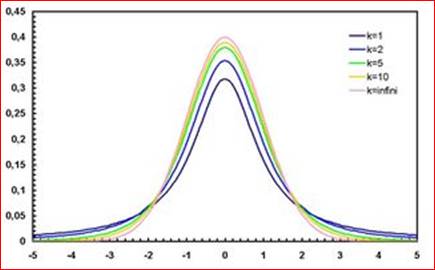
La loi de Student.
La loi de Student est une loi de probabilité, faisant intervenir le quotient entre une
variable suivant une loi normale centrée réduite et la racine carrée d'une
variable distribuée suivant la loi du χ².
Soient Z une
variable aléatoire de loi normale centrée et réduite et U une
variable indépendante de Z et distribuée suivant la loi la loi du
χ² à k degrés de liberté. Par définition la variable
T = ![]()
suit une loi
de Student à k degrés de liberté.
La densité
de T notée ƒT est :
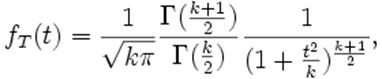 pour k ≥ 1.
pour k ≥ 1.
où Γ
est la fonction Gamma d'Euler.
La densité
ƒT associée à la variable T est symétrique, centrée sur 0, en forme de cloche.
Son espérance ne
peut pas être définie pour k = 1, et est nulle pour k > 1.
Sa variance est infinie pour k ≤ 2 et vaut 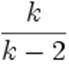 pour
k > 2.
pour
k > 2.
Tables : il existe des tables donnant p( |X|
> x) selon la valeur de k .
|
De la loi de student à la loi
normale : Lorsque n ® ¥ on admet que la loi de Student converge vers
la loi N(0,1) |
.
Application : détermination rigoureuse de
l’intervalle de confiance associé à l’espérance d’une variable de loi normale
de variance inconnue
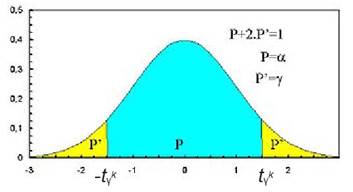
Student à k
degrés de liberté. ![]() est la valeur de t pour laquelle P(t>
est la valeur de t pour laquelle P(t>![]() )= y
)= y
Si x1,…xn
suivent une loi normale d'espérance e (à déterminer) et de variance σ2
(inconnue) , au niveau de confiance c , e appartient à l'intervalle
[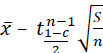 ,
, 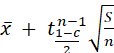 ]
]
avec ![]() =moyenne des Xi et S estimateur de e =
=moyenne des Xi et S estimateur de e = ![]()
r =1– c est
le risque de l'estimation.
Loi de
student à n – 1 degrés de liberté.
![]() est la valeur T de la table pour
laquelle Pr(t >T) =
est la valeur T de la table pour
laquelle Pr(t >T) = ![]()