INTEGRATION

Primitives

Définition : F(x) primitive de f(x) définie sur [a,b] ⇔ F(x) dérivable sur [a,b] et f(x) est la dérivée de F(x) .

● Si F(x) est une primitive de f(x) , F(x) + K en est une autre (K = constante)

● toutes les primitives de f sont de la forme F(x) + K

● f(x) continue admet au moins une primitive

● Il existe une seule primitive F(x) de f(x) telle que F(a)=b

Exemples

● x² est une primitive de 2x . x² + 5 aussi .

● -1/x est une primitive de 1/x² .

Tableau de primitives (à une constante près)

(x–a)^a a ≠ –1			tan x		Arg th x
aÎR	ln | x – a |		–		Arc tan x
cÎR	ln |x - c|		ln | tan |		Arc sin x
ln x	X (ln x -1)		ln |tan ()|		Arg sh x	ln(x+)
e^c^x		Coth x	ln | sh x |		Arg ch x	ln(x+)
tan x	–ln |cos x|	th x	ln ch x		–Arg th x	–

Nous noterons ∫ f(x) une primitive de f(x). Mais, dans le cadre de ce cours, de manière implicite nous considèrerons que F(x) est une primitive de f(x), G(x) une primitive de g(x) etc …

∫ cos x = sin x + C et plus généralement ∫ f(x) = F(x) .

Intégrales

Considérons les graphes de f(x) définie et continue sur [a,b] (figure 1) et de sa primitive F(x) , (figure 2) .

Sur les 2 graphiques , découpons l'intervalle [a,b] en segments de longueur Dx, dont les extrémités sont x_i et x_i+1.

Sur la figure 1 , les rectangles situés sous la courbe de f(x) forment une aire totale S_Dx = (1)

Sur la figure 2 , on s'intéresse aux triangles situés sous la courbe de F(x) (qu'on a grossi sur la figure 3) .

Leur hauteur , BH=DF_i est variable mais si on appelle a_i le coeff directeur de AB , on a la relation BH = (a_i)AH.

soit DF_i = (a_i)Dx .

La somme des hauteurs de ces triangles est = F(b)-F(a). (2)

On a donc sur la figure 1 : S_Dx = (1) et sur la figure 2 : = F(b)-F(a). (2)

Si maintenant , on fait tendre Dx vers 0 , il existe une valeur dx de Dx assez petite pour que S_Dx de la figure 1 soit très voisine de l'aire S représentée sur la figure 4 .

Pratiquement , on n'a plus des valeurs différenciées x₁ , x₂ etc... mais un tissu continu de valeurs de x, si bien qu'on abandonne la notation S de la somme (1) pour adopter la suivante :

S=

qu'on lit somme (ou integrale) de f(x).dx quand x varie de a à b .

Si l'on revient aux figures 2 et 3 , lorsque Dx tend vers 0 , la droite AB , sécante par rapport à la courbe, tend vers la tangente à la courbe . Le coefficient directeur de AB qui est (a_i) tend donc vers le coefficient directeur de la tangente qu'on sait être le nombre dérivé au point d'abscisse x_i : (a_i)→ F'(x_i) = f(x_i) (F étant une primitive de f) .

Comme précédemment, on peut considérer que DF_i et Dx tendent respectivement vers des valeurs dF et dx qu'on appelle différentielles d'une fonction et de sa variable . Elles sont liées par la relation : dF=F'(x).dx= f(x).dx .

Là aussi , on peut abandonner la notation S de la somme (2) pour la notation intégrale en remplaçant tan(a_i)Dx par f(x).dx ce qui donne :

F(b)-F(a)=

.

Si on identifie ce résultat et le résultat précédent , on découvre que l'aire S de la figure 4 (comprise entre la courbe f(x) , l'axe des abscisses et les droites x=a et x=b) est égale à F(b) -F(a) . F(x) étant une primitive de f(x) .

S = F(b) - F(a) encore noté ou simplement [F]

La notion d'aire algébrique :

S =

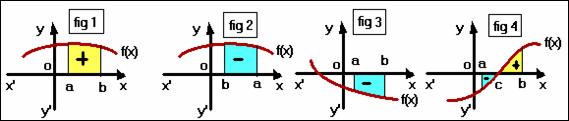
On considère que dx est positif quand a< b et négatif quand a>b . Quant au signe de f(x) , il peut varier sur [a,b].

Ainsi , l'aire S pourra, selon le cas, être positive ou négative .

Fig 1) a<b (dx positif) et f(x) positif sur [a,b] donc S positif .

Fig 2) a>b (dx négatif) et f(x) positif sur [a,b] donc S négatif

Fig 3) a<b (dx positif) et f(x) négatif sur [a,b] donc S négatif

Fig 4) a<b (dx >0). Sur [a,c] f(x) <0 on obtient une aire négative -S1 et sur [c,b] une aire positive S2. S=S2-S1

Propriétés de l'intégrale

= -

= + (relation de Chasles)

= +

(linéarité)

= K

| | £ (valeur absolue de la somme inférieure à la somme des valeurs absolues. Voir fig 4)

Intégrale et moyenne

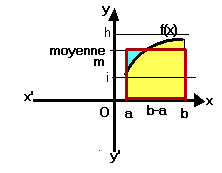
Quelle que soit l'aire S= , il existe une valeur moyenne m telle que l'aire du rectangle de largeur m et de longueur (b - a) soit égale à S.

m(b-a) = .

On a donc m = = . m est la moyenne de f sur [a,b] .

Si pour tout x de [a,b] on a : i ≤ f(x) ≤ h . on peut écrire i ≤ m ≤ h

Donc on peut encadrer l'intégrale : i(b-a) ≤ ≤ h(b-a) .

Techniques d’intégration

Changement de variable

Sous l'intégrale on peut avoir f(x)dx ou f(t)dt , ce qui équivaut à un simple changement de nom de la variable et ne change pas la valeur de l’intégrale.

Mais si t et x sont des variables différentes, on ne sait pas calculer l'intégrale de f(x)dt ou de f(t)dx .

On a vu qu'entre une fonction et sa variable existe la relation df = f '(x).dx .

Donc si dans f je procède à un changement de variable, x est une fonction x(t) de t, et on a,

en tout point du domaine d’intégration dx = x’(t)dt et f(x) = g(t) ,

g(t) étant la fonction obtenue à partir de f par le changement de variable t = t(x).

En règle générale, dans f on remplace une expression en x par t, donc on ne définit pas x(t) mais plutôt t(x) et il faut commencer par calculer x(t) avant de pouvoir calculer x’(t)dt.

Mais attention aux bornes de l'intégrale : si, par exemple, x varie initialement de a à b , t variera de t(a) à t(b) . Finalement, on a :

1) Dans f, on fait un changement de variable f(x) = g(t).

2) on remplace dx par x’(t).dt .

3) on s’assure qu’on sait calculer la primitive de g(t).x’(t).

4) on remplace les bornes de l’intégration en x par les bornes de l’intégration en t et on procède au calcul

Exemple : soit à calculer I=.

On sait que est une primitive de x². Mais quelle est la primitive de (3x+2)² ?

Essayons le changement de variable t = 3x+2 .

En appliquant dt=t'(x).dx il vient dt = 3 dx ou dx=dt/3 .

Et on pourra transformer (3x + 2)² en t² = g(t).

Sous l'intégrale on aura donc ∫ 1/3 (t)².dt qu'on transformera en 1/3 ∫ t²dt.

Et cette fois, on connaît la primitive de t²

Mais attention si x varie de 1 à 3 , t = 3x + 2 varie de 5 à 11 . On obtient :

I = 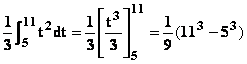que nous vous laissons le soin de calculer.

Intégration par partie (i.p.p)

La méthode découle du constat suivant : si u et v sont des fonctions de x , on a (u.v)' = u'v + v'u .

En appliquant la formule df=f'dx on trouve d(uv) = (uv)'dx = (u'v + vu')dx = u'vdx + uv'dx .

En passant aux intégrales , on a ∫ d(uv) = ∫ (u'vdx + uv'dx) = ∫ u'vdx + ∫ uv'dx .

Et comme ∫ df = [f] on a ∫ d(uv) = [uv] (Si on intègre sur [a ; b] : [uv] = (uv)(b) – (uv)(a)) .

La formule i.p.p à retenir est donc [ uv ] = ∫ u’vdx + ∫ uv'dx

Pour mener à bien une intégration par parties, il faut déterminer deux fonctions u et v telles que

1 I = ∫ f(x)dx = ∫ uv'dx et …

2 Soit nous connaissons une primitive de u’v , soit nous savons évaluer ∫ u’vdx en fonction de I

● Dans [ uv ] = ∫ u’vdx + ∫ uv'dx on remplace ∫ uv'dx par I l’intégrale cherchée,

et comme le calcul de [ uv ] est trivial, si celui de ∫ u’vdx ne pose pas de problème nous sommes tirés d’affaire.

● La première exigence est toujours remplie en posant par exemple u=f(x) et v'dx=dx ce qui donne v'=1 c’est à dire v=x . On a donc : u=f(x) u'=f'(x) v=x v'=1.

Si f(x) est un produit de fonctions usuelles comme dans I = , on peut choisir soit

u = x et v’ = cos x, soit u = cos x et v’ = x . En général, ce choix n’est pas indifférent.

● Mais on doit connaître la primitive de u’v . Ou l’on doit savoir exprimer ∫ u’vdx en fonction de I (par exemple sous la forme λI) . Si ce n’est pas le cas, inutile d’aller plus loin. À moins qu’une nouvelle intégration par parties, cette fois sur ∫u’vdx finisse par déboucher.

Exemple : calculer I = . On ne connaît pas la primitive de xcosx.

On essaie une intégration par parties : on pose u=x , v'=cosx donc on évalue u'= 1 et v = sinx .

On connaît la primitive de u’v = sin x , donc applique la formule i.p.p :

[xsinx] = ∫ sinx dx + ∫ x cosx dx ⇨ I = [xsinx] – ∫ sinx dx = [xsinx] – [−cosx]

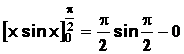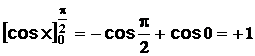= et donc

I =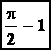

fonctions rationnelles

Cas particuliers

P est un polynôme de R[X] et P’ sa dérivée

● La primitive de est ln |P| Exemple : = ln | x² + 5| = ln (x² + 5)

● La primitive de est Exemple :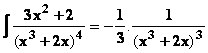

● Les fonctions contenant des exponentielles (e^ax) se ramènent au cas général par le changement de variable

t = e^ax d’où on tire dt = at.dx et par conséquent dx = dt ce qui nous fait souvent déboucher sur l’intégration d’une

fraction rationnelle une fois le changement de variable opéré.

Exemple :

Décomposition en éléments simples de 1^ere espèce dans C

Voir cette décomposition dans le cours d’algèbre : chapitre polynômes et fractions rationnelles.

Dans C on peut écrire toute fraction rationnelle sous la forme

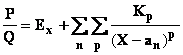où E_x est un polynôme (partie entière de la fraction),

les a_n sont les racines réelles ou complexes de Q , les K_p sont des coefficients réels ou complexes selon la nature de la racine qui figure au dénominateur, l’exposant p varie de 1 à la multiplicité des racines.

Par exemple, si a_n est une racine triple on trouvera dans la somme 3 termes de la forme suivante :

Supposons que les racines soient réelles (les k_i le sont aussi)

● ∫ E_X ne pose pas de problème puisque E_x est un polynôme

● = K₁ ln | X – a_n |

●

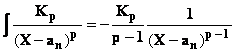
Donc, nous savons intégrer

Supposons que les racines simples soient complexes (les k_i le sont aussi)

En posant a_n = a + ib, en séparant partie réelle et partie imaginaire notre problème se ramène au suivant : Quelle est la primitive de  ?

On trouve (tableau des primitives)

Lorsque est à coefficients réels, les termes complexes sont conjugués et les parties imaginaires finissent par

s’annuler.

Eléments simples de seconde espèce

● Etudions d’abord la forme avec b²–4ac < 0 et n entier naturel non nul.

On pose aX²+bX+c = a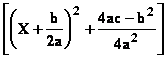 puis y = x + et enfin t = y

Le calcul de In = est ramené au calcul de J_n = = ò f(t,n) dt

En intégrant par parties (u = 1/(t² +1)ⁿ et v’ = 1) on trouve une formule de récurrence :

J_n = 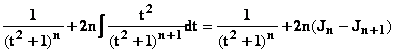soit 2nJ_n+1 = (2n-1)J_n + f(t,n)

On a donc :

J₁ = = Arc tan t et la formule de récurrence nous donnera de proche en proche J₂ , J₃ , …

● On peut aussi faire le changement de variable t = tan u et on trouve

In = (voir plus loin les intégrales de ce type)

● Etudions maintenant la forme .

Il suffit d’écrire le numérateur sous la forme X = pour décomposer notre forme en deux formes que nous savons intégrer, l’une étant la forme précédente et l’autre la forme .

● Exemple : calculer I =

La partie entière de la fraction E_x est nulle (d° du numérateur < d° du dénominateur)

Les pôles simples de la fraction sont 2 et 3 donc I = = –7 ln |X–2| +9 ln |X – 3|

● Une astuce, souvent utile : faire apparaître au numérateur le facteur qui figure au dénominateur

I= 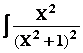→ on écrit X² = (X² + 1) –1 et on scinde I en 2 fractions facilement intégrables

I= 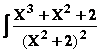→ on écrit X³+X²+2 = X³+2X -2X+ X²+2 = X(X²+2) +(X²+2) –2X

et on obtient 3 fractions facilement intégrables.

● procéder à un changement de variable

I = en écrivant I en fonction de y =X² la décomposition en pôles simples est plus facile

I = 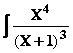le seul pôle étant 1 , en écrivant I en fonction de y = X+1 on simplifie l’étude

I = en posant u = X³ on aura et sera plus facilement décomposable

● notre but est de nous rapprocher au dénominateur de 1± X, 1± X² à une constante prés avec un numérateur de degré inférieur , car les primitives connues ont cette forme.

Intégrales trigonométriques

On a à intégrer ∫ f(cos x , sin x) dx , f étant un polynôme ou une fraction rationnelle

Méthode générale :

Si on pose t = tan(x / 2) on peut écrire

Sin x = Cos x = Tan x =

et de x=2Arc tan t +2kπ on déduit dx =

Dés lors, f est transformée en une fraction rationnelle en t et notre étude rejoint la précédente.

Simplifications :

● Si f(x)dx=f(–x)d(–x) (f impaire) on posera u = cos x → x = Arc cos u → dx = (-1 / )du

● Si f(x)dx = f(π – x)d(π – x) , on posera u = sin x → x = Arc sin u → dx = ( 1 / )du

● Si f(x)dx = f(π + x) d(π + x) on posera u = tan x → x = Arc tan u → dx = (1/ (1+u² ) du

Attention : Il faut que ces fonctions soient bijectives sur les intervalles d’intégration pour que les fonctions réciproques soient définies.

Primitives de ∫ sin px cos qx ∫ sin px sin qx ∫ cos px cos qx où p et q sont entiers.

On a

● sin a cos b = [ sin (a+b) + sin (a–b)]

● sin a sin b = [ cos (a–b) – cos (a+b)]

● cos a cos b = [ cos (a+b) + cos (a–b)]

À partir de là, on sait faire.

Primitives de la forme ∫ cos ^p x sin ^q x ou ∫ cos ^p x ou ∫ sin ^p x où p et q sont des entiers

On utilise les formules d’Euler cos x = et sin x =

On développe cos ^p x et (ou) sin ^q x , on regroupe les termes qui ont des exposants opposés et on obtient pour chaque développement une somme de termes de la forme å a _k cos kx ou å b _k sin kx.

Dés lors, on retombe sur une forme de primitive connue ,

soit ∫ Σ a _k cos kx ,

soit ∫ Σ b _k sin kx

soit ∫ Σ a _k b _k’ (sin k ’x) (cos kx)

Exemple : cos³ x = ()³ = (e^i3x + 3e^i2xe^-ix + 3^eixe^-2ix + e^-3ix)

= = .

On sait calculer une primitive de cette expression et si on la multipliait par sin ^p x sous la même forme, le produit obtenu ne poserait pas plus de problème puisqu’on sait intégrer ∫ sin px cos qx

Primitives de la forme I_n = ∫ cos ^{– n} x ou J_n = ∫ sin ^{– n} x où n est un entier naturel

● Si n est pair , on pose n = 2p puis on pose t = tan(x )

I_2p = ∫ (1+t²) ^{p –1}dt : un polynôme qu’on développe avant de l’intégrer.

En particulier si p = 1 :

Pour calculer J_2p on commence par le changement de variable y = π/2 – x : sin (π/2 – y) = cos y

Ce qui nous ramène au cas précédent.

● Si n est impair , on pose n = 2p +1

Pour J_2p+1 on procède au changement de variable t = tan (x / 2) J_2p+1=

Une fraction rationnelle simple à décomposer et à intégrer pour p petit (dénominateur en t ^k).

Par exemple : = ln |t| = ln |tan (x/2)|

Le calcul de I_2p+1 se ramène au précédent en posant y = π/2 – x : cos (π/2 – y) = sin y

Par exemple = – ln |t| = – ln |tan (y/2)| = – ln |tan (π/4 – x/2)|

Primitives de la forme I_n = ∫ tan ⁿ x où n est un entier

● Si n est négatif on pose y = π/2 – x et tan ⁿ x = tan ^{– n} y (on retrouve le cas où n est positif)

● Si n est positif et impair n = 2p +1 on pose t = cos 2x : I_2p+1=

On procède à un autre changement de variable u = 1 + t qui nous permet de décomposer facilement

I_2p+1 en intégrales simples.

● Si n = 1 il est plus simple de faire le changement de variable t = cos x

Puisque tan x = et dt = – sin x dx on a ò tan x = – = – ln |t| = – ln |cos x|

● lorsque n est positif impair ou pair on peut aussi poser t = tan x et on a I_n = dt .

Une fois calculée la partie entière de la fraction, son reste est facile à intégrer .

Par exemple t³ = (1 + t²) t –t. La partie entière de la fraction est t et on connaît la primitive de –.

C’est –.

Intégrales de Walis

I_m = où m est un entier naturel

On pose u = sin^m–1x et v’=sinx → u’ = (m-1)(cos x) (sin^m–2 x) et v = cos x

D’où l’on déduit : I_m = [ – sin ^m–1x cos x ] _{(0 , π/2)} + I_m–2

I_m = I_m–2

Comme I₀ = et I₁ = 1

● si m est pair  (m=2p) on a I_m =

● Si m est impair (m = 2p+1) on a I_m =

Avec :

2x4x6x..x2p = 2 ^p (p ! )

Et 3x5x7x..x(2p–1) =

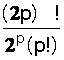
Remarquons que = (changement de variable x = – u )

On montre, en encadrant les intégrales que I_m est une suite décroissante et que lim (I_m+1 / I_m) = 1

Donc 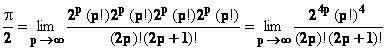= (2p+1) lim ( I_2p+1)² et I_n ≈

Primitives d’expressions avec radicaux

Nos primitives de référence sont

Arcsin x

Arccos x

Arg sh x

Arg ch x

Avec, si l’on veut Arg sh x = ln |x+| et Arg ch x = ln |x+| et |x| ≥ 1

● Plus généralement , si k est une constante et u une variable

Arc sin (●)

Arc cos

Arg sh

Arg ch ( ●)

(●) avec k > u (●) avec u > k

Avec si l’on veut Arg sh = ln |u + | et Arg ch = ln |u + |

Primitives de la forme

● Si a = 0 la primitive est

● si a ≠ 0 on écrit le polynôme sous la forme a [ ( ] soit a [u² ± K²] et la solution est triviale.

Primitives de la forme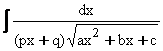

On se ramène au cas précédent en posant t = → et x=

Finalement on doit intégrer –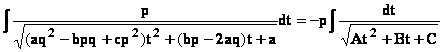

Primitives de la forme

● Si a = 0 la primitive est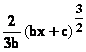

● Si a ≠ 0 , on écrit le polynôme sous la forme a [u² ± K²] ou si a < 0 : |a|[ K² ± u²]

Selon ce qu’il y a sous le radical, on fait les changements de variables suivants qui nous ramènent à des intégrales connues :

● → on pose = sin t et on a cos² t sous le radical → k² ∫ cos² t dt = ∫ (1+cos 2t) dt

● → on pose = sh t et on a ch² t sous le radical →k² ∫ ch² t dt = ∫ (1+ch 2t) dt

● → on pose = ch t et on a sh² t sous le radical →k² ∫ sh² t dt= ∫ (ch 2t – 1) dt

Primitives de la forme ou où f est une fraction rationnelle.

On prend pour variable u = → x = et dx=

Ce qui nous ramène à l’intégration d’une fraction rationnelle.

Primitives de la forme où f est une fraction rationnelle

On met le polynôme sous le radical sous la forme canonique et selon sa forme :

● → on pose = sin t et on a cos² t sous le radical

● → on pose = sh t et on a ch² t sous le radical

● → on pose = ch t et on a sh² t sous le radical

Il nous reste une fraction rationnelle avec des formes trigonométriques ou hyperboliques qu’on devrait savoir résoudre, au prix d’un nouveau changement de variable.