Analyse combinatoire

L’analyse combinatoire permet le dénombrement d’ensembles formés par des groupements d’éléments obtenus à partir d’autres ensembles. Les probabilités reposant le plus souvent sur le dénombrement, ces techniques d’évaluation du nombre vont nous être très utiles.

Groupement ordonné ou non ordonné

Soit un ensemble de deux éléments on le note { x ; y } et on l’appelle un doubleton.

Si maintenant cet ensemble de 2 éléments peut être considéré comme un choix, un prélèvement ou un tri parmi les éléments d’un ou plusieurs ensembles plus vastes on l’appelle soit un couple noté (x,y) , soit une paire notée {x,y} .

˜ On l’appelle paire si {x ;y} et {y ;x} constituent le même élément.

Par exemple

Sur un ensemble de n chevaux, j’en choisis 2 {x, y } pour les vendre.

Je tire 2 boules sur n dans une urne l’ordre dans lequel je les tire étant sans importance

˜ On l’appelle couple si (x ;y) et (y ;x) ne constituent pas le même élément. L’ensemble est ordonné.

Par exemple

x est le 1^er d’une course et y le second (x,y) est donc l’ordre inverse de (y,x)

x Î un ensemble E , y Î un ensemble F Au contraire de (x,y) , (y,x) situerait y dans E et x dans F

x et y sont les coordonnées d’un point (x,y) n’est pas le même point que (y,x)

On peut procéder avec n éléments comme on vient de le faire avec 2 .

Pour 3 éléments on va parler de triplet ordonné (x ;y ;z) et de tripleton non ordonné {x;y;z}

Plus généralement un groupement ordonné de n éléments est appelé un n – uplet .

Dénombrement d’un ensemble produit

E contient n éléments

F contient p éléments

Je peux créer des couples d’éléments (x , y) tels que x Î E et y Î F

L’ensemble de tous ces couples est appelé ensemble produit de E par F ( noté E x F)

E F	X1	…	Xn
Y1	(X1 ;Y1)		(Xn ;Y1)
…
Yp	(X1,Yp)		(Xn ;Yp)

Combien de couples puis je créer de cette façon ?

n.p

(d’où le nom d’ «ensemble produit »)

Par exemple

˜ E est un ensemble de 10 hommes, F est un ensemble de 8 femmes et E x F l’ensemble des couples (homme, femme) que l’on peut former à partir de ces 2 ensembles. On compte 8x10 = 80 couples possibles.

˜ Dans un repère cartésien, le plan est l’ensemble des points de coordonnée (x,y) tel qu xÎR et yÎR , il s’agit donc de l’ensemble produit R x R noté R². Ici on ne peut les compter, il y en a un infinité. On dit que l’ensemble n’est pas dénombrable.

On peut aussi définir l’ensemble produit E x F x G comme l’ensemble des 3 – uplets (x ;y ;z) tels que xÎE , yÎF, zÎG.

Si E contient n éléments, F contient p éléments, G contient q éléments, combien de 3 – uplets contient

E x F x G ? n.p.q

Plus généralement

On peut constituer des ensembles produits E1 x E2x…x En à partir de n ensembles (n≥2).

L’ensemble produit E1 x E2x…x En est l’ensemble des n-uplets (X1 ; X2 ; …Xn) tels que

X1 ÎE1 ; X2ÎE2 ; …XnÎEn.

Le cardinal (nombre d’éléments) de l’ensemble produit est égal au produit des cardinaux des n ensembles constitutifs.

˜ Je tire une boule bleue dans une urne qui en contient 10, une boule blanche dans une urne qui en contient 3, une boule rouge dans une urne qui en contient 5. Combien de tirages (bleu, blanc, rouge) sont possibles ?

10x3x5 = 150 tirages possibles en tout.

˜ En base 4 les chiffres sont {0, 1 , 2, 3} combien de nombre de 4 chiffres puis je former de 0000 à 3333 ?

4 x 4 x 4 x 4 = 256.

Permutations d’un ensemble ordonné de n éléments

Soit un ensemble de 3 éléments {1,2 ;3} .

Combien de façon d’ordonner les 3 éléments existe-t-il ?

1 en premier

(1,2,3) 2 en second

(1,3,2) 3 en second

2 en premier

(2,1,3) 1 en second

(2,3,1) 3 en second

3 en premier

(3,1,2) 1 en second

(3,2,1) 2 en second

Le nombre de possibilité en fonction de la place de rangement est

En 1^er nous avons 3 possibilités

En 2^e pour chaque 1^er choisi il reste 2 possibilités

En 3^e pour chaque couple (1^er , 2^e ) choisi il ne reste qu’une seule (1) possibilité

Donc en tout nous avons 3 x 2 x 1 = 6 possibilités de rangement.

Plus généralement :

Soit un ensemble de n éléments.

On appelle permutations toutes les possibilités de ranger ces n éléments dans un ordre quelconque.

Le nombre de permutations possibles, noté P_n est n x (n–1) x (n – 2) x …. X 3 x 2 x 1

Le nombre n ! = n x (n–1) x (n – 2) x …. X 3 x 2 x 1 est appelé factorielle n

Attention ! Par convention on décide que 0 ! = 1

On sait que 3 chevaux sont arrivés en tête d’une course mais on ne sait pas dans quel ordre.

Combien d’ordres possibles pour ces 3 chevaux ?

3 ! = 3 x2 = 6

Combien de classements possibles pour une classe de 10 élèves ?

10 ! = 10 x 9 x 8 x 7 x 6 x 5 x 4 x 3 x 2 = 3 628 800

Combien de mots de 5 lettres possibles en permutant les 5 lettres du mot ABCDE ?

5 ! = 5 x 4 x 3 x 2 = 120 mots

Arrangements p à p de n éléments d’un ensemble

Supposons maintenant que dans un ensemble de 10 élèves je veuille faire tous les classements possibles de 3 élèves. Combien puis je en faire ?

En 1ere position j’ai 10 possibilités

En 2^e position il ne me reste que 9 possibilités quand j’ai choisi le 1^er

En 3^e position il ne me reste que 8 possibilités quand j’ai choisi le 1^er et le 2^e .

Le nombre cherché que l’on appelle « arrangements de 10 élèves 3 par 3 » et que l’on note

est donc égal à = 10 x 9 x 8

Notons que si a , b et c sont 3 élèves, l’arrangement (a, b , c) est différent par exemple de (a, c , b) .

Le terme arrangement suggère que l’ordre a de l’importance. Ce sont les triplets formés de 3 éléments différents que nous comptons (les classements (a,a,a) ou (a,a,b) par exemple n’auraient aucune signification) .

Notons aussi que = 10 x 9 x 8 x 7.

Plus généralement :

Soit un ensemble de n éléments.

Si je veux les grouper p par p (avec 0< p ≤ n) de telle sorte que la modification de l’ordre au sein d’un groupe débouche sur la création d’un groupe différent , le nombre de groupes ordonnés ainsi réalisables, s’appelle « nombre d’arrangement de n éléments p à p » et il est noté .

Exemple :

J’ai 5 boules numérotées 1 ; 2 ; 3 ; 4 ; 5. et 3 boites de couleurs différentes Rouge , Vert , Bleu .

Je tire 3 boules au hasard que je cache et que je mets chacune dans un boite de couleur différente.

Il faut deviner quelle boule contient chaque boîte.

Combien de possibilités a le joueur ?

Je peux écrire qu’une solution est du type R = 2  ; V = 5 ; B = 1 , ou (2 ; 5 ; 1) un triplet où la 1ere place est celle de la boite Rouge, la 2^e place celle de la boite Verte et la 3^e place celle de la boite Bleue.

Bien sûr (1 , 2 , 5) est différent de (2 , 5 , 1) puisque au moins une boite ne contient pas la même boule.

Il me faut donc chercher le nombre d’arrangements des 5 boules 3 par 3.

On peut dire que le joueur, a possibilités soit 5 x 4 x 3 = 60 possibilités.

Combinaisons p à p de n éléments d’un ensemble

Supposons maintenant qu’avec ma classe de 10 élèves, je veuille faire des groupes de 3 élèves qui vont se rendre à tour de rôle à la bibliothèque.

Combien de groupes puis je former ?

Cette fois, l’ordre n’a aucune importance {a ; b ; c} est le même groupe que {a ; c ; b} .

On appelle ce type de groupe où l’ordre n’a aucune importance une « combinaison » .

Le nombre de combinaison de 10 élèves 3 par 3 est noté . C’est le nombre recherché.

Avec une combinaison de 3 élèves , combien puis je faire d’arrangements de 3 élèves ?

Il y a 3 ! = 6 façons de permuter ces 3 élèves au sein d’une combinaison, pour obtenir chaque fois des arrangements différents.

Donc on aura 6 fois moins de combinaisons que d’arrangements.

On a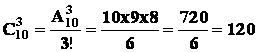

Plus généralement :

Soit un ensemble de n éléments.

Si je veux les grouper p par p (avec 0< p ≤ n) de telle sorte que l’ordre au sein du groupe n’ait aucune importance, le nombre de groupes non ordonnés ainsi réalisables, s’appelle « nombre de combinaisons de n éléments p à p » et il est noté

Dans une urne 5 boules numérotées 1 ; 2 ; 3 ; 4 ; 5

Je tire au hasard 3 boules et je les mets dans une boite. Il faut deviner le numéro des boules contenues dans la boîte.

Combien de possibilités ?

Je peux faire en tout combinaisons de boules

Pour visualiser toutes les combinaisons, on numérote arbitrairement les objets, puis on les utilise dans l’ordre croissant pour combler les places vacantes. Le no des boules doit augmenter selon leur rang (leur place) .

123 1 en 1^e position / 2 en 2^e position / on va épuiser toutes les solutions en 3^e place

124

125 plus de solution en 3^e place , on augmente le numéro de la boule en 2^e place

134 3 en 2^e position / on va épuiser toutes les solutions en 3^e place

135 plus de solution en 3^e place , on augmente le numéro de la boule en 2^e place

145 4 en 2^e position , 5 en 3^e position , on augmente le numéro de la boule en 1^e place

234 2 en 1^e position / 3 en 2^e position

235

245 plus de solution en 2^e/3^e place , on augmente le numéro de la boule en 1^e place

345 3 en 1^e position / 4 en 2^e position / 5 en 3^e position. Plus de solution. On arrête.

Et on compte en tout 10 combinaisons

Permutations dans plusieurs sous groupes indépendants

Un ensemble ordonné a la configuration suivante :

3 symboles Ì «M occupent les 3 premières places

5 lettres A , B , C , D , E occupent les 5 places suivantes

8 chiffres 1 , 2 , 3 , 4 , 5 , 6 , 7 , 8 occupent les 8 dernières places.

Chaque élément pouvant changer de place parmi celles qui lui sont dévolues ,

Voici,par exemple, un ordre possible pour cet ensemble :

MÌ « C A B E D 7 1 2 4 8 5 3 6

De combien de façon puis je ordonner cet ensemble ?

Il y a

3 ! façons d’ordonner les 3 symboles

5 ! façons d’ordonner les 5 lettres

8 ! façons d’ordonner les 8 lettres

Comme chaque permutation de symboles peut être associée à une permutation de lettres , elle-même associée à une permutation de chiffres , on a en tout :

N = 3 ! 5 ! 8 ! associations possibles.

Plus généralement

Quand l’ordre au sein d’un ensemble E est lié aux permutations de plusieurs de ses sous ensembles indépendants.

Si l’effectif des sous ensembles permutants est respectivement n₁, n₂ , …. , n_k.

Le nombre de permutations possibles dans E est

Exemple le carnaval est formé du défilé à la queue leu leu et dans cet ordre de 3 fanfares, 4 géants, 12 chars.

Combien de façons d’organiser le défilé ?

Réponse N = 3 ! 4 ! 12 !

Permutations comprenant des objets identiques

Combien de nombres différents de 5 chiffres peut – on faire avec les chiffres 11123 ?

1) on suppose que les 5 chiffres sont différents : 1a , 1 b , 1c , 2 , 3 .

2) Dans ce cas on formerait 5 ! permutations possibles de ces 5 chiffres soit 5 ! nombres différents.

3) Le problème est que dans notre cas , toutes les permutations qui voient les 1 à la même place sont équivalentes. Par exemple (1a, 2, 1b , 3, 1c) est équivalente à (1c , 2 , 1a , 3 , 1b) car ces 2 permutations forment le même nombre 12131.

4) combien de permutations sont équivalentes au nombre 12131 ? Il suffit de laisser les 1 , le 2 , le 3 à la même place et de permuter les indices des 1 (a, b , c) ce qui donne 3 ! permutations équivalentes .

5) Donc, selon le même principe, chacun des nombres cherchés est équivalent à 3 ! permutations parmi les 5 ! initiales.

6) Si N est le nombre cherché on a donc (3 !)N = 5 ! ou = 5 x 4 = 20

Supposons maintenant qu’il y ait plusieurs groupes d’objets équivalents .

Par exemple combien de mots différents de 8 lettres peut on faire avec ABBCDEEE ?

En tout on aurait 8 ! permutations en considérant que toutes les lettres seraient différentes .

Mais il faut diviser ce nombre

˜ par le nombre de permutations du groupe B B : 2 ! = 2

˜ Par le nombre de permutations du groupe EEE : 3 ! = 6

On a donc = 8 x 7 x 6 x 5 x 2 = 3360

Plus généralement

Soit un ensemble E de n éléments contenant un ou plusieurs groupes g₁ , … g_k d’objets identiques.

Supposons que le groupe g_i contienne n_i objets identiques

Le nombre de permutation dans le groupe g_i serait n_i ! si ses objets étaient tous différents.

Le nombre P de permutations différentes de l’ensemble E est

Une portion de gène contient

38 nucléotides a , 10 nucléotides b et 12 nucléotides g

Sachant que chaque nucléotide peut occuper n’importe quelle place sur le brin, combien y a-t-il de configurations différentes possibles pour le brin ?

Réponse : P =

Propriétés

Par exemple

En effet à chaque combinaison de p objets sur n (par exemple de 5 objets sur 9) correspond la combinaison des n–p objets restants (par exemple des 4 objets restants sur 9). Il y a donc autant de combinaisons de n objets p à p (9 objets 5 à 5) que de n objets n – p à n – p (9 objets 4 à 4).

1 2 3 4 5 6 7 8 9

En bleu une combinaison de 5 objets sur 9 , en jaune la combinaison complémentaire de 4 objets sur 9 qui lui correspond.

Par exemple

1 2 3 4 5 6 7 8 9

Il y a en tout combinaisons de ces 9 objets 5 par 5.

Parmi ces combinaisons il y en a qui ne contiennent pas le 1. Combien ?

Puisqu’il reste 8 objets (2 3 4 5 6 7 8 9 ) à combiner 5 par 5 .

Parmi ces combinaisons il y en a qui contiennent le 1. Combien ?

Puisque chaque combinaison de 5 objets contenant le 1 est obtenue par adjonction au 1 d’une combinaison de 4 objets sur les 8 restants.

On a donc bien

Formule du binôme de Newton

(a+b)⁴ = (a+b)(a+b)(a+b)(a+b)

1 2 3 4 les facteurs sont numérotés de 1 à 4 .

Je sais qu’en développant je vais obtenir des a⁴ , des a³b , des a²b² , des ab³ et des b⁴.

Mais combien de chaque catégorie ?

Quel est le coefficient de chaque terme dans la somme

(a+b)⁴ = .. a⁴ + .. a³b + .. a²b² +.. ab³ +.. b⁴ ?

Je vais obtenir un a³b, par exemple, en combinant les a de 3 facteurs avec le b du facteur restant.

Par exemple : en combinant le a des facteurs nos 1 3 4 et le b du facteur no 2

Combien de combinaisons de facteurs 3 à 3 puis je faire avec mes 4 facteurs :

Le coefficient de a³b dans la formule est donc

En complétant toute la formule par le même procédé on va trouver

(a+b)⁴ = a⁴ + a³b + a²b² + ab³ b⁴.

ou

(a+b)⁴ = 1 a⁴ + 4 a³b + 6 a²b² + 4 ab³ + 1 b⁴.

Plus généralement :

Formule du binôme :

de cette formule on déduit la propriété suivante :

Considérations sur la formule du binôme.

Les exposants décroissent pour a (de n à 0) et croissent pour b (de 0 à n)

On rappelle que X⁰ = 1 et on remarque que

La somme des exposants de a et de b reste égale à n dans tout terme.

Le coefficient d’un terme est . Pour p on peut prendre aussi bien l’exposant de a que celui de b puisque l’un est p et l’autre n – p et que le nombre de combinaisons est le même si on change p par n–p .

Les coefficients sont symétriques par rapport au centre de la formule (le 1^er est égal au dernier, le second à l’avant dernier etc ..)

Le premier et le dernier coefficients sont toujours 1 .

Le second et l’avant dernier coefficients sont toujours n .

Triangle de Pascal

p de è	0	1	2	3	4	5	6
(a+b)^1	1	1						a+b
(a+b)^2	1	2	1					a^2+2ab+b^2
(a+b)^3	1	3	3	1				a^3+3a^2b+3ab^2+b3
(a+b)^4	1	4	6	4	1			a^4+4a^3b+6a^2b^2+4ab^3+b^4
(a+b)^5	1	5	10	10	5	1		a^5+5a^4b+10a^3b^2+10a^2b^3+5ab^4+b^5
(a+b)^6	1	6	15	20	15	6	1	a^6+6a^5b+15a^4b^2+20a^3b^3+15a^2b^4+6ab^5+b^6

C’est une façon très simple et pratique de calculer les coefficients de (a+b)ⁿ à partir de ceux de (a+b)¹.

Sur la première ligne, à partir de (a+b) = a + b on écrit les coefficients du binôme qui à ce stade sont

1 et 1.

On sait que le développement de (a+b)ⁿ comprend n+1 termes et que le premier et le dernier coefficients seront des1.

À partir de là, pour trouver n’importe quel coefficient (case verte) on additionne 2 coefficients de la ligne au dessus : celui qui est juste au dessus du coefficient à calculer et celui qui est tout de suite à gauche de ce dernier (cases bleues) .

Par exemple, pour trouver le 10 de la ligne (a+b)⁵ on a ajouté le 6 et le 4 de la ligne au dessus.

On peut ainsi construire tout le triangle des coefficients jusqu’à la ligne qui nous intéresse.

Cette façon de procéder est justifiable par la formule :