Le sens de la mesure , c'est d'abord le sens de l'histoire .
Au fond , il n'est pas illogique de constater que l'évaluation de distances de plus en plus grandes a coïncidé avec l'avènement d'époques de plus en plus récentes .
Ceci dit , on verra que les procédés les plus anciens ne sont pas forcément les moins élégants .
Comment faisait - on pour calculer le rayon terrestre au deuxième siècle avant Jésus - Christ ?
N'êtes vous pas curieux d'apprendre comment on calcule la distance d'une étoile , sa masse , son champ magnétique ou son diamètre alors que même les plus puissants télescopes n'en donnent qu'une image ponctuelle?
Les anciens et la mesure du monde
Les Egyptiens maîtrisaient déjà les techniques de la mesure mais ils les utilisaient surtout dans la vie pratique , pour leurs constructions , leurs actes de propriété ou le calcul de leurs impôts.
Leurs notions de géométrie étaient rudimentaires . Elles étaient basées sur des constatations pratiques , sans fondement scientifique . Par exemple , ils utilisaient un ancêtre du théorème de Pythagore qui approchait d’assez prés la réalité grâce à un savant bricolage .
Ils voyageaient peu par la mer, même si l’on prête à l’un de leurs pharaons , Néchao 1er , d’avoir organisé le premier tour de l’Afrique en navire. Or , l’on sait que la navigation maritime est un bon stimulant pour l’astronomie et les sciences qui s’y rattachent .
Ils utilisaient surtout leurs connaissances astronomiques aux fins d’établir des calendriers et des horoscopes ou prédire les crues du Nil . Mus par leurs préoccupations économiques et religieuses , ils s’intéressaient surtout à la zone de l’écliptique.
On leur doit quand même le système sexagésimal (basé sur le nombre soixante) dont on a hérité la mesure des angles en degrés et les divisions du temps en heures , minutes et secondes .
Et aussi le vin millésimé qu’il stockaient en indiquant l’année de la récolte .
Ce n’est déjà pas si mal pour un début .
Les mesures à grande échelle débutèrent sérieusement avec l’école grecque d’Alexandrie au deuxième siècle avant Jésus Christ , plus de mille ans après les balbutiements égyptiens.
Supposons qu'on vous demande de mesurer la circonférence de la Terre avec un mètre de couturière .
Vous vous insurgeriez probablement contre la tache titanesque qu'on vous aurait fixée .
C'est pourtant , à peu prés, ce qu'a fait Eratosthène . Son astuce nous laisse pantois .
|
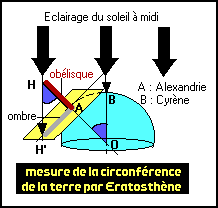
Remarquant qu’en été à midi , le soleil se trouvait au Zénith à Cyrène , alors que sa hauteur était moins importante à Alexandrie , (les deux villes étant distantes d’environ 800km) Eratosthène imagina un moyen de calculer la circonférence de la Terre et d’en déduire son rayon.
Connaissant la hauteur de l’obélisque d’Alexandrie et la longueur de son ombre à midi , il lui fut facile de calculer l’angle H qu’il évalua à 7,2° .
Ayant admis le caractère sphérique de la Terre , et le parallélisme des rayons lumineux , provenant du Soleil, sur toute sa surface , il était facile d’en déduire que l’angle H était égal à l’angle O qui intercepte l’arc de grand cercle (AB) qui relie les deux villes .
La mesure de l’angle O (7,2°) étant égale au cinquantième de l’arc total (360°) , le tour de la Terre devait mesurer 50 fois 800 km soit 40.000 Km .
En réalité , Eratosthène , qui mesurait en stades (1 stade = 315 m) trouva une circonférence de 39500 km .
Même si cette mesure , étonnamment précise , devait beaucoup à la chance , on appréciera l’ingéniosité de la méthode et l’on n’oubliera pas que lorsque Christophe Colomb partit découvrir l’Amérique , 17 siècles plus tard , il avait en tête que le monde était beaucoup plus petit que ne l’indiquait la mesure d’Eratosthène .
|
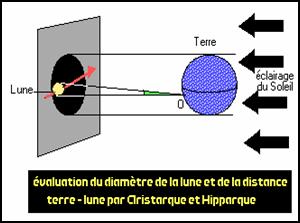
C’est Aristarque de Samos , (celui là même qui conçut le premier système héliocentrique) , qui inventa cette méthode de calcul du rayon de la Lune et de sa distance à la Terre .
Il supposa que , compte-tenu de la distance à laquelle est situé le Soleil , le cône d’ombre de la terre est en fait un cylindre .
Cela signifie que le cercle d’ombre traversé par la Lune les soirs d’éclipse a les mêmes dimensions que la Terre.
En faisant le rapport entre le diamètre de la Lune et le diamètre de ce cercle , à l’occasion d’éclipses, on trouve 0,27 (soit environ ¼) . On en déduit que la Lune est quatre fois plus petite que la Terre .
Ce rapport est celui entre le temps que met la lune pour
entrer dans le cercle et le temps qu'elle y reste .
Puis , évaluant à environ 30 minutes d’angle le diamètre apparent de la Lune et sachant qu’une grandeur de 1 mètre est vue sous un angle de 30 minutes quand on est situé à 120 mètres d’elle , on trouve que la Terre devrait se situer à 120 fois ¼ de diamètre terrestre de la Lune (30 diamètres ou 60 rayons Terrestres ).
Ce calcul, qui dépend évidemment de la précision avec laquelle on a évalué les dimensions de la Terre , pourrait donner environ 380.000 Km de qui serait assez proche de la réalité (384.000 km) .
En réalité , les chiffres donnés par Aristarque et corrigés par Hipparque étaient plus éloignés de la réalité car ils avaient sur - évalué le diamètre de la lune, respectivement à la moitié et au tiers du diamètre du disque d'ombre.
Mais leurs méthodes étaient géniales et forcent le respect .
Aux 16eme et 17eme siècle
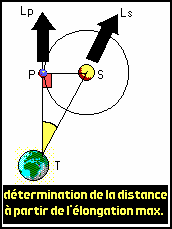
Entre autres avantages , le système de Copernic , en prenant le Soleil comme centre, permettait d’affirmer que lorsque l’élongation d’une planète inférieure (l’angle T du dessin) était maximale, la phase (angle P du dessin) était égale à 90 ° (en effet TP est tangent à l’orbite de P) .
La phase de 90° (qui correspond à un éclairage de la moitié de la planète semblable au quartier de Lune) ne sera observée qu’un peu plus tard grâce au télescope de Galilée et de toute façon , il aurait été difficile de la mesurer avec précision .
|
Pour ce qui est de l’élongation , il n’est pas question de la mesurer directement puisque le Soleil et la planète ne sont pas visibles simultanément .
Mais , en imaginant la sphère céleste en arrière fond , on devine que l’élongation correspond à la différence absolue des longitudes écliptiques du soleil (Ls) et de la planète (Lp) . Il est donc facile d’évaluer la valeur maximale prise par l’angle T et d’en déduire que ce jour là , l’angle P est égal à 90° .
En connaissant les rudiments de la trigonométrie , on détermine facilement que :
TP = ST cos(T) et SP=ST sin(T) .
SP et ST sont à peu prés fixes , puisqu’il s’agit du rayon des orbites mais TP varie en fonction de la date . Il est facile d’évaluer TP dans toutes les positions de P quand on connaît le rapport entre SP et ST et la période des planètes .
Ainsi , on pouvait calculer toutes ces grandeurs en fonction de ST qu’on appelle aujourd’hui Unité Astronomique (UA) .
Mais il faudra attendre encore un peu pour traduire l’UA en kilomètres ou dans une unité de mesure en vigueur au 17eme siècle .

Avec une planète supérieure , nous savons que l’angle P de phase ne dépasse jamais une valeur maximale (inférieure à 50°) .
Il faudrait donc que l’on puisse évaluer la position de la planète qui donne un angle droit , non plus en P mais en S (Terre en A) . Mais cela n’est pas aisé .
Aussi , nous admirerons la méthode adoptée par Kepler qui consiste à relever les longitudes écliptiques de la planète et du soleil Lp(A) et Ls(A) quand la Terre se trouve en A (quelconque) et à recommencer l’opération après que la planète ait effectué une révolution complète sur son orbite et se retrouve au même endroit .
A ce moment là , la Terre se trouve en B et les longitudes sont Lp(B) et Ls(B) . La différence des longitudes du Soleil |Ls(A) - Ls(B)| donne l’angle ASB .
De plus, SAP=|Ls(A) -Lp(A)| et SBP=|Ls(B) - Lp(B)| .
On peut donc reconstituer une figure à l’échelle et calculer toutes les distances en fonction de la distance SA (rayon de l’orbite terrestre = 1UA) .
Quand Kepler aura trouvé sa 3eme loi : T2/a3 =K (constante) , on pourra se dispenser de cette gymnastique puisqu’il suffira de connaître la période (T) pour en déduire la mesure du demi grand axe (a). En effet , si a est le demi grand axe (en UA) et T la période de la planète (en années) le cas de la Terre prouve que K=1.
Newton corrigera cette loi en précisant qu’en réalité c’est l’expression (M+m) T2/a3 qui est constante . (M étant la masse du Soleil et m celle de la planète) . Mais m est tellement petit devant M, le rapport étant inférieur à 1 pour 1000 , que la formule donnée par Kepler constitue une bonne approximation de la réalité .
Voyons maintenant comment évaluer les rapports de masses à partir des principaux résultats de Newton :
Si un corps tourne autour d’un autre à une distance D , avec une période T , une vitesse linéaire V et une vitesse angulaire w=2p/T , on peut calculer l’accélération g qu’il subit de la part de la masse centrale de plusieurs façons :
g = K V2/d , g = K w2d ou g = K 4p2d/T2 (1) (K étant une constante dépendant des unités choisies) .
Ce résultat vaut pour l’accélération exercée sur la terre par le soleil (G) et pour celle exercée sur la lune par la terre (g). Si la lune tourne à une distance d de la terre en un temps t , tandis que la terre tourne à une distance D du soleil en un temps T , on peut lier les accélérations à partir de (1) par la relation G=g![]() (2).
(2).
Autre résultat : la force exercée par la terre sur le soleil est égale à la force exercée par le soleil sur la terre .
Si m est la masse de la terre , M la masse du soleil , G l’accélération exercée par le soleil sur la terre et g celle exercée par la terre sur le soleil , on a la relation mG = Mg. En éliminant G dans (2), on trouve 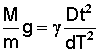 (3).
(3).
Reste à éliminer g et g de (3) , ce qu’on fait en disant que les accélérations exercées par un même corps (la terre) sur un astre situé à une distance D (le soleil) et un corps situé à une distance d (la lune) sont liées par la relation :
 . Finalement , on trouve la relation entre les masses du soleil (M) et de ma terre (m) :
. Finalement , on trouve la relation entre les masses du soleil (M) et de ma terre (m) : 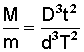 .
.
D, d, t et T étant connus, on peut calculer que M = m . 329100 . Connaissant ce rapport, il suffit d’utiliser la 3eme loi de Kepler transformée par Newton pour étendre ce résultat à toutes les planètes.
18eme et 19eme : les siècles de parallaxe
Nous avons vu dés le premier chapitre que , pour observer un objet éloigné sous deux directions différentes , il faut effectuer un déplacement important .
Plus l’objet est éloigné , plus l’écart entre les lieux d’observation doit être grand et plus les techniques d’observation doivent être précises et donc sophistiquées .
|
Cela explique qu’historiquement , on ait commencé par mesurer les distances à la Lune et aux planètes avant les distances aux étoiles et les distances aux étoiles avant les distances aux galaxies .
Ce dessin relate un épisode de l’astronomie datant du 18eme siècle .
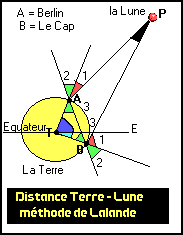
Lalande et La Caille se sont rendus l’un à Berlin (Allemagne) et l’autre au Cap (Afrique du Sud) pour mesurer la distance de la Terre à la Lune .
Le même jour , à la même heure , ils visent la Lune avec leurs instruments et évaluent l’angle de leur visée avec la verticale du lieu (ou l’horizontale , ce qui revient au même) . Ces angles , colorés en rouge, sont notés A1 et B1.
Les deux villes (A et B) étant sur le même méridien , il est facile d’évaluer l’angle T = ATB qui est égal à la somme de leurs latitudes (Nord et Sud) .
Le triangle TAB étant isocèle , on n’a aucune difficulté à déterminer la valeur des angles colorés en vert , qui sont tous égaux à (180 - T) / 2 .
Les angles A3 et B3 sont respectivement égaux à (180 - B1 - B2) et
(180 - A1 - A2) . Donc , ils n’offrent aucun mystère .
Pour le reste , on peut faire confiance aux mathématiciens : lorsqu’ils savent construire une figure à l’échelle , ils savent calculer toutes ses dimensions et en particulier , la distance TP qui nous intéresse .
On notera qu’ici , la distance TP est largement inférieure à ce qu’elle serait sur un dessin à l’échelle (60 fois AT le rayon terrestre) . Si on avait donné à TP sa dimension exacte , les droites AP et BP seraient presque parallèles , et les angles qu’elles feraient avec la droite AB seraient presque égaux (B1+B2 » A3) .
Comme on a P = 180 - B3 - A3 = (B1+ B2) - A3 , on voit que si les astronomes mesuraient l’angle que fait leur ligne de visée avec la droite AB , ils trouveraient l’un B1+B2 et l’autre A3 , la différence de leurs mesures serait égale à l’angle P . Ici , la différence de leurs mesures serait de l’ordre de 2 degrés mais pour le soleil , elle serait à peine de l’ordre de 5 millièmes de degrés (18’’ d’angle) . Une précision que les instruments du 18eme siècle ne pouvaient garantir . Le soleil étant à 8 minutes lumière contre 4,5 années lumières pour l’étoile la plus proche , il n’était pas question , à cette époque , de mesurer la distance aux étoiles .
|
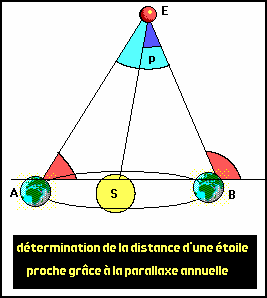
Pour cela , il a fallu attendre que la mesure des angles gagne en précision et qu’on sache prendre comme base deux lieux A et B éloignés non pas d’un diamètre terrestre mais d’un diamètre de l’orbite terrestre . Deux lieux diamétralement opposés de part et d’autre du soleil .
Inutile de dire qu’ici , les visées ne sont pas simultanées : six mois les séparent dans le temps . Mais comme l’étoile dont on veut mesurer la distance est supposée fixe , cela n’a pas d’importance .
La base AB mesure cette fois 300.000.000 km au lieu d’un maximum de 13.000 km dans le cas précédent .
Malgré cela , pour l’étoile importante la plus proche (Toliman) l’angle E (= B - A) mesure moins de 2 secondes d’arc .
C’est dire la précision requise par les mesures que des phénomènes optiques comme l’aberration visuelle ou la réfraction atmosphérique viennent fausser .
L’angle P (qui est à peu prés égal à la moitié de l’angle E) est l’angle sous lequel on voit le rayon de l’orbite terrestre depuis l’étoile .
On l’appelle parallaxe annuelle . Si il était égal à 1 seconde , la distance de l’étoile serait 1 parsec .
Toliman est à 1,3 parsecs de la Terre ( P < 1 ’’) .
Au delà de 100 parsecs , cette méthode n’est plus utilisable.
Nous savons que , pour un angle a trés petit , on peut considérer que sin (a)=a évalué en radians .
On en déduit que P = SB/SP et si l’on mesure SB et SP en U.A , SB = 1 et SP = d . Donc P = 1/d ou d=1/P.
Il suffit d’inverser la parallaxe (calculée en radians) pour trouver la distance en U.A .
On rappelle que 1pc = 3,262 al = 206225 UA
et que 1’’ d’angle = 0,000004849 radians=1 / 206225 radians
On en déduit que la formule P = 1/d est aussi valable quand P est exprimé en secondes et d en parsecs .
Actuellement , donc , la limite de la méthode (100 pc) correspond à une parallaxe P de 1 centième de seconde.
En 1781 , les progrés de l’optique et la chance permirent à Herschel de découvrir Uranus, la septième planète.
La huitième et la neuvième seront préssenties par le calcul avant d’être réellement observées .
La résolution du difficile problème des 3 corps (quelle est l’influence combinée du soleil et de la planète à découvrir sur l’orbite de la planète observée? ) permit ces exploits consacrant le triomphe de la mécanique newtonienne .
En étudiant les perturbations des trajectoires des planètes supérieures , Le Verrier et Adams prédirent l’existence de Neptune avant qu’elle soit observée en 1846 .
En 1930 , Lowel déduisit du calcul l’existence de Pluton , avant qu’elle soit découverte par Tombaugh, sur un cliché photographique .
20eme : le siècle de la lumière
Au 20eme siècle , les théories de Planck et d’Einstein modifièrent complètement notre approche de la lumière .
Sa dualité , d’onde et de corpuscule (le photon) , favorisa l’interprétation de nombreux phénomènes .
Les développements de la relativité eurent de nombreuses retombées sur l’astronomie . On put formuler des théories cohérentes sur la nature du big-bang , les réactions dont les étoiles sont le siège , l’existence des trous noirs , l’influence de la masse sur la lumière , le déplacement du périhélie des planètes , le comportement des objets situés dans des champs gravitationnels intenses , etc ..
Parallèlement , les développements technologiques nous dotèrent d’outils permettant d’accroître démesurément la gamme de nos perceptions . Antennes radio , Radars , Télescopes hyper - puissants , satellites ou sondes spatiales, caméras CDD , spectroscopes , interféromètres , (...) , nous fournirent une moisson de données de toute sorte que l’informatique nous permit d’exploiter pour des résultats extrêmement féconds .
L’astronomie d’aujourd’hui ressemble , en somme, à une chauve - souris déployant ses énormes oreilles pour capter tous les bruits provenant de l’univers et les soumettre à un cerveau trés performant pour en traduire la complexité en une image cohérente et directement exploitable.
|
Aux 19eme et 20eme siècle , les progrès de la spectroscopie stellaire et les lois de Doppler-Fizeau , permirent de mesurer les vitesses des mouvements propres des étoiles qui se traduisent par des déplacements presque imperceptibles (quelques secondes d’arc par an) sur la sphère céleste .
On détermina ainsi que le système solaire se déplaçait lui même vers un point appelé Apex , situé quelque part dans la constellation de la Lyre .
Toutes les étoiles situées en direction de l’Apex semblent se rapprocher de nous en s’écartant de notre trajectoire , comme les arbres , sur le bord d’une route rectiligne quand nous la parcourons en voiture . Pour les étoiles situées dans la direction opposée (l’Antapex) , elles s’éloignent en se rapprochant de l’axe de notre mouvement , conformément à ce que l’on doit observer pour les arbres si l’on regarde par la lunette arrière du véhicule .
On déduisit de ce mouvement propre du soleil que la trajectoire réelle de la Terre n’était pas une ellipse mais une hélice s’enroulant autour de la trajectoire du soleil comme un escalier en colimaçon .
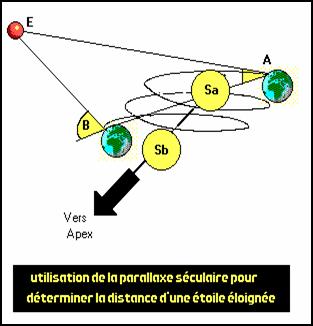
Cela nous donnait l’occasion de définir une base AB de parallaxe beaucoup plus grande qu’un diamètre de l’orbite terrestre . Il suffisait d’attendre suffisamment longtemps , entre deux observations (entre A et B) , pour que la terre ait parcouru plusieurs pas sur la spirale .
Mais cette méthode comporte un inconvénient manifeste : s’il faut attendre plusieurs années entre A et B pour que le soleil se soit significativement déplacé (on parle de parallaxe séculaire) , l’étoile E en a fait autant et l’on ne peut prétendre , lorsqu’on la vise en B , qu’elle se trouve au même endroit que lorsqu’on la visait en A .
En conséquence , on ne peut utiliser cette méthode que lorsqu’on l’applique non pas à une étoile individuelle mais à un amas sphérique situé très loin , au dessus du disque galactique . Dans un tel amas , on considère que toutes les étoiles ont des déplacements propres isotropes de moyenne nulle , ce qui fait que la méthode permet de calculer la moyenne des distances des étoiles de l’amas qu’on définit comme la distance à l’amas.
En clair , cela signifie que si l’on fait une erreur +Dd dans l’évaluation de la distance d’une étoile , ce n’est pas grave car pour une autre étoile de l’amas , on a probablement fait une erreur -Dd qui annule la précédente .
On comprend pourquoi ce procédé, dit « des courants d’étoiles », est généralement considéré comme peu fiable .
La dernière tentative d'utiliser la parallaxe pour mesurer les distances se releva donc moins fertile que les précédentes .
Les procédés purement optiques , qu’on va examiner maintenant sont à peu prés de la même veine , mais ils donnent une idée de l'évolution des techniques et de l'absence de limites de l'ingéniosité humaine .
Les méthodes optiques
C'est Pickering (Harvard) qui, à la fin du siècle dernier, commença à différencier les spectres stellaires selon la présence de certaines raies d'absorption ou d'émission et à les ranger en classes spectrales.
L'une de ses collaboratrices , Antonia Maury , procèda à un classement plus fin en sous - classes , en fonction de la netteté des raies , ce qui déplut à Pickering mais passionna Hertzprung (Danemark) qui , en 1905, remarqua qu'il existait un rapport entre la netteté des raies et la luminosité intrinsèques .
De façon générale , les raies d'étincelle (provenant d'atomes ionisés) , sont d'autant plus nettes que l'étoile est lumineuse et les raies d'arc (provenant d'atomes neutres) sont d'autant plus nettes que la luminosité est faible .
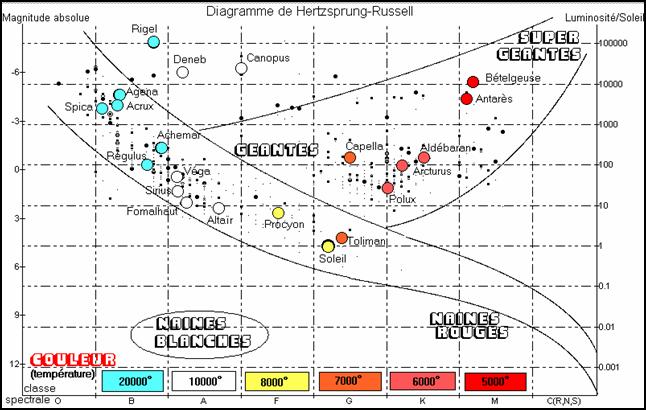
En 1913 , Russel (Princeton) , qui a pris connaissance des travaux de Hertzprung et s'est lié d'amitié avec lui , publie un diagramme qui permet de lier la classe spectrale , la taille , la température de surface , la couleur et la magnitude absolue des étoiles . Il associe son ami à sa publication .
Du bas vers le haut , les étoiles peuvent être classées par taille et luminosité croissantes .
De gauche à droite , on les classe par couleur (du bleu vers le rouge) et température décroissante .
Les classes spectrales coïncident avec un ou deux domaines très réduits du diagramme(de tailles ou de magnitudes différentes mais de température et de couleur semblables, par exemple , classe M : super géantes et naines rouges).
Les sous-classes permettent un classement plus fin sur l'échelle des magnitudes.
La magnitude absolue du soleil est 4,7 . Les étoiles les plus brillantes , situées dans le haut du diagramme , brillent comme cent mille ou un million de soleils . Leur magnitude absolue est environ -9 .
Les étoiles les moins brillantes brillent cent mille fois moins que le Soleil et leur magnitude absolue est 17.
Le calcul de certaines magnitudes découle d'une extrapolation .
La magnitude apparente (m) , est évaluée directement en mesurant l'effet provoqué par la lumière provenant de l'étoile sur une cellule photo électrique . On la connaît précisément pour toutes les étoiles .
La magnitude absolue (M) étant la magnitude apparente qu'aurait l'étoile si elle était à une distance de 10 parsecs il existe une relation mathématique entre les deux : M = m + 5 - 5 log d .
Il suffit de connaître deux des 3 grandeurs liées par cette relation (m , M , d) pour calculer la 3eme .
Pour les étoiles les plus proches , on peut évaluer la distance grâce à la méthode des parallaxes, puis vérifier que la magnitude absolue calculée par ce procédé correspond à la valeur déterminée par la méthode des classes spectrales . Cela permet d'étalonner le dispositif .
Pour les étoiles très éloignées (en gros plus de 100 parsecs) dont la parallaxe est très petite , en utilisant le diagramme d'Hertzprung - Russel , on peut évaluer la magnitude absolue (M) de l'étoile qui va permettre à son tour de calculer sa distance à la Terre .
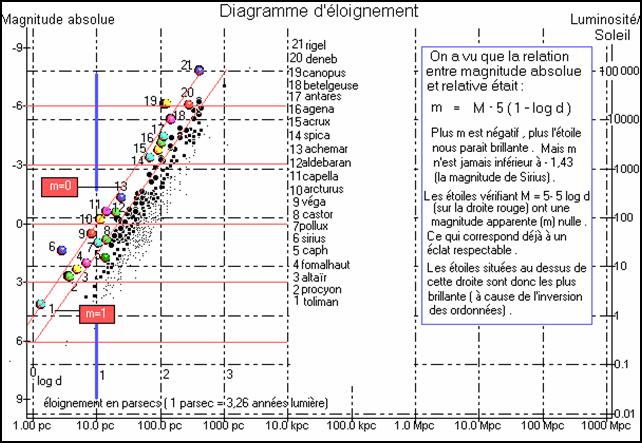
Ici , les couleurs attribuées aux étoiles importantes n'ont aucun rapport avec la réalité . Elles servent surtout à les distinguer les unes des autres .
Ce diagramme d'éloignement permet de situer les étoiles les plus connues (qui sont aussi souvent les plus lumineuses) .
Grâce à lui , on peut aussi évaluer leur magnitude absolue (échelle de gauche) ou leur luminosité par rapport au soleil (échelle de droite) .
Pour classer les étoiles selon leur magnitude apparente , il faut tracer des droites obliques parallèles à celles qui figurent sur le schéma .
A l'ordonnée à l'origine égale à 5 correspond la magnitude apparente 0 , à l'ordonnée à l'origine 6 correspond la magnitude apparente 1 , ainsi de suite .
L'apparente concentration des étoiles dans une bande oblique tient donc à ce que seules les étoiles de magnitude inférieure à 4 ont été représentées . Si l'on était monté plus haut dans l'échelle des magnitudes , le nuage de points aurait recouvert une plus grande partie du plan .
Néanmoins , si l'on considère que la taille des symboles d'étoiles est fonction de la magnitude apparente , on constate que les symboles de même taille sont bien distribués parallèlement aux droites obliques d'isomagnitude.
Les galaxies
Pour clore ce chapitre sur l'évaluation des distances , il faut dire un mots des galaxies .
Pour déterminer la distance des galaxies les plus proches , on utilise les étoiles variables appelées Céphéides .
Elles ont ceci de particulier que la connaissance de leur période permet de calculer leur magnitude absolue et donc d'en déduire leur distance .
Il a fallu attendre les années 50 pour affirmer que la grande nébuleuse d'Andromède (l'objet le plus lointain qu'on puisse voir à l'œil nu) était en réalité une galaxie deux fois plus grande que la nôtre (qui mesure déjà 100.000 années lumière de diamètre) . Bien que située à deux millions d'années lumière , elle est très proche puisqu'elle appartient au groupe local (avec les galaxies du nuage de Magellan , plus petites) .
Pour déterminer la distance de galaxies , plus lointaines , quand on ne distingue plus les céphéides , on se base sur la magnitude des étoiles les plus brillantes (dont on a auparavant étalonné l'éclat grâce aux étoiles comparables des galaxies les plus proches) , ou sur leur vitesse de rotation autour du noyau .
Enfin , quand on ne distingue plus aucune étoile , on se fie à la luminosité globale de la galaxie .
Ainsi , au fur et à mesure que la distance augmente , son évaluation est soumise à une incertitude de plus en plus grande qui atteint assez rapidement l'ordre de grandeur de la mesure elle même .
Cela ne décourage pas pour autant les astronomes qui savent qu'il faut entreprendre pour réussir .
Distance et céphéides
En 1784 , un jeune astronome amateur , Goodricke découvre dans la constellation de Céphée, une étoile (Delta Céphéi) dont l'éclat varie régulièrement dans le temps . Plus tard , on observera d'autres étoiles du même type qu'on baptisera "céphéides" . Puis d'autres types de variables physiques (par exemple RR Lyrae) .
La taille et la luminosité des céphéides oscillent avec un léger déphasage . On observe un maximum de luminosité un peu avant que la taille soit maximale et un minimum de luminosité un peu avant que la taille soit minimale (Les RR Lyrae varient de façon moins régulière) .
Les céphéides ont des périodes différentes allant de 1 à 70 jours (moins de 1,5 jours pour RR Lyrae) .
On sait aujourd'hui que ce comportement est dû à une instabilité des couches internes des étoiles .
Leur noyau d'hydrogène est entièrement transformé en Hélium et en se déplaçant vers une couronne moins profonde , cette réaction entraîne une augmentation de la pression gazeuse sur les couches externes qui provoque la dilatation , bientôt contrariée par l'énorme force gravitationnelle du noyau , responsable de la rétractation et de l'accroissement de l'opacité par ionisation des couches d'hélium .
|
Petit et grand nuage de Magellan sont deux galaxies irrégulières de l'amas local (donc assez proches de la nôtre) , visibles depuis l'hémisphère sud de la terre et découvertes par le navigateur Portugais lors de son tour du monde en 1520 .
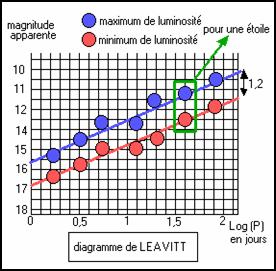
En 1912 , Henriette Leavitt étudie les céphéides du petit nuage de Magellan. Elle découvre une relation linéaire entre le logarithme de la période des céphéides et leur magnitude apparente au maximum de luminosité (courbe bleue) ou au minimum (courbe rouge) . Les 25 céphéides étudiées ont des magnitudes apparentes relativement faibles (de 10 à 16) et il est manifeste que plus la période de leur clignotement est grande , plus leur éclat est grand (ou leur magnitude faible) .
Comme le petit nuage de Magellan est relativement réduit , au regard de la distance qui nous sépare de lui , on peut admettre que ces étoiles sont toutes approximativement situées à la même distance et qu'il doit exister une relation du même type entre leur luminosité (leur magnitude absolue) et leur période .
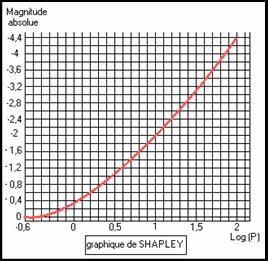 Cette relation sera quantifiée en 1918 par Shapley .
Cette relation sera quantifiée en 1918 par Shapley .
Il avait connaissance des travaux de Hertzsprung et Russel et appliqua leur méthode (ainsi que d'autres de son crû) à la détermination des magnitudes absolues et distances de céphéides.
Une fois qu'on savait évaluer les magnitudes et la distance de certaines céphéides , il était facile de les lier à la période pour étalonner la loi de Leavitt , puis , en extrapolant, de déduire de la période (dont la détermination ne pose aucun problème) , à la fois la magnitude absolue et la distance de toutes les céphéides.
Le graphique de Shapley montre comment varie la magnitude absolue d'une céphéide (à son maximum d'éclat) en fonction de sa période . De la magnitude absolue (M, déduite du graphique) et de la magnitude apparente (m, facilement mesurable) , on déduit la distance grâce à la loi maintenant familière :
M = m + 5 - 5 log(d) .
On put calculer à l'époque que la galaxie d'Andromède était située à 900.000 années lumière de la terre (qu'on ramena à 680.000 en1930) et les nuages de Magellan à 80.000 années lumière .
|
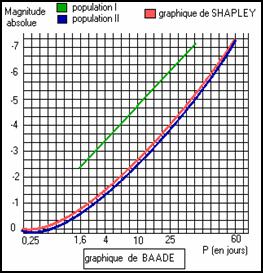
En 1952 , un américain , Walter Baade fit une découverte qui remit fortement en question les résultats de Shapley : il y avait deux types de céphéides (différenciés par leur spectre) et pour l'un d'eux (le type W Virgini), la relation période luminosité de Leavitt , que Shapley avait cru pouvoir généraliser , devait être corrigée .
Si l'étoile contient presque exclusivement de l'hydrogène et de l'hélium, ce qui est le cas des céphéides des amas globulaires , la loi de Shapley (courbe rouge) est valable .
Mais si la céphéide contient d'autres corps (notamment des métaux), il faut faire correspondre à la période une magnitude absolue inférieure de 1,5 à ce qu'elle serait dans le graphique de Shapley (courbe verte) . Du coup , il fallait situer la galaxie d'Andromède à 2.200.000 d'années lumière et le petit nuage de Magellan à 250.000 années lumière. Leur distance avait plus que doublé .
En permettant de calculer la parallaxe de certaines céphéides, les satellites Hubble et Hipparcos confirmèrent que cette loi paraissait exacte à 5 ou 10% prés.
Le redshift (Z)
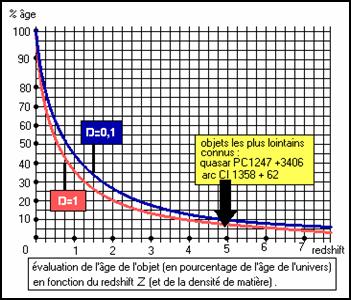
L’âge de l’univers , son rayon de courbure , son avenir dépendent apparemment de 3 paramètres :
l la constante de Hubble (H) nous renseigne sur la vitesse d’expansion de l’univers : 2 galaxies distantes de d mégaparsecs s’éloigneraient mutuellement l’une de l’autre à la vitesse v=Hd.
Après de nombreux tâtonnements , les mesures de H semblent converger vers 72 km/s/Mpc.
l Le paramètre de densité (W) est égal au rapport de la densité D de l’univers à une valeur critique Dc La valeur de W influe à la fois sur la courbure et le scénario d’évolution de l’univers .
Si W est entre 0 (exclu) et 1 (inclus) , l’expansion de l’univers sera infinie . Si W > 1 l’univers se contractera après une phase d’expansion .
Pour l’instant on évalue W entre 0,1 et 1 mais on aimerait bien qu’il soit égal à 1 (D=Dc) , ce qui confèrerait à l’univers une courbure nulle .
lLa constante cosmologique (L) peut également influer sur les dimensions et la forme (si elle est non nulle) en modulant les effets des forces de gravitation. Mais son utilité est incertaine .
|
Nous pouvons mesurer le décalage spectral des objets lointains qui s’éloignent de nous à la vitesse v.
Dl/l.=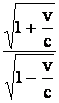 . Et on pose Z=Dl/l.- 1 .
. Et on pose Z=Dl/l.- 1 .
Z est appelé « redshift » . Plus il est grand , plus la vitesse de fuite des objets est grande et plus leur éloignement dans l’espace et le temps est grand, lui aussi, conformément à la loi de Hubble. Mais il n’est cependant pas possible d’évaluer leur distance ou leur âge à partir de Z car cette évaluation est fonction du modèle d’univers adopté . Faute de mieux, le graphique ci – contre permet d’évaluer le pourcentage de l’âge de l’univers qu’on peut attribuer à l’objet en formulant pour W deux hypothèses (W=0,1 et W=1). Mais l’âge de l’univers demeure inconnu . On le pense compris entre 10 et 15 milliards d’années .
|
Un pourcentage de 0% de l’âge de l’univers correspond au big-bang et 100% à l'instant actuel (distance nulle). Théoriquement , Z peut prendre des valeurs largement supérieures à 1000 .
Mais on voit sur le graphique que Z = 0,5 correspond déjà à 50% de l'âge de l'univers soit une distance de 5 à 7,5 milliards d'années lumière selon les estimations actuelles.
Les plus gros redshifts mesurés actuellement pour des objets identifiés (autour de 5) les situent à moins de 10% de l'âge de l’univers soit entre 9 et 13 milliards d'année lumière .
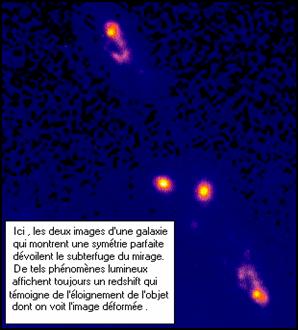
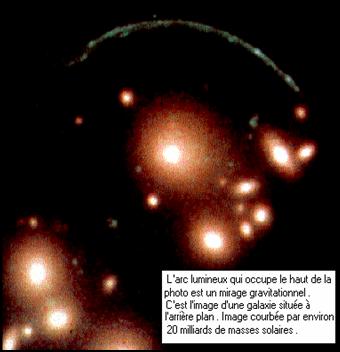
Certaines galaxies se comportent comme des lentilles gravitationnelles. Elles amplifient la lumière émise par des objets très lointains (qui sans elles seraient invisibles) et en déforment les images qui parviennent jusqu’à nous sous forme d’arcs , de croix ou de mirages multiformes .
Les photos illustrant ce chapitre en donnent deux illustrations remarquables .
Il ne faut donc pas s'étonner si parmi les objets les plus lointains dont on ait mesuré le redshift on trouve un quasar (l'objet le plus lumineux) et un arc gravitationnel .
Mais le record de distance évolue tous les ans et l’avenir nous réserve encore de belles surprises .
Masse , diamètre : les étoiles doubles
On dénombre plus de 70.000 étoiles doubles dans les catalogues .
On évalue entre 40 et 50 % la proportion des étoiles multiples par rapport au nombre total d'étoiles .
La plupart sont des étoiles doubles . Certaines sont si proches qu'elles échangent de la matière , ce qui constitue un spectacle fascinant , mais pour la plupart d'entre elles , les couples sont suffisamment séparés pour que rien de tel ne se produise . Les étoiles doubles tournent autour de leur centre gravité commun (G) , la moins massive (appelée compagnon) ayant le plus grand rayon orbital , ce qui la fait tourner autour de la plus massive .
Les couples optiques permettent de calculer la masse des étoiles.
|
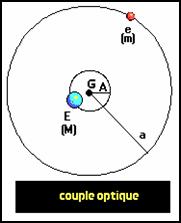
On parle de couple optique (E,e) lorsque les deux orbites sont intégralement visibles . On en dénombre environ 600 , ce qui est relativement peu .
Dans ce cas , connaissant la distance du couple à la Terre , on peut évaluer les rayons a et A de leurs orbites autour de G , le demi grand axe a de l'orbite de e autour de E et sa période p .
Les lois de la gravitation universelle donnent : M/m = a/A et M+m = a3/p2.
A partir de là , il est facile de calculer les masses respectives M et m des étoiles.
Ce calcul a été mené pour une cinquantaine d'étoiles et a permis d'étalonner la relation (linéaire) entre masse et luminosité découverte par Eddington en 1924.
Cette relation permet à son tour d'évaluer la masse d'étoiles dont on connaît la luminosité , mais elle n'est pas applicable aux géantes rouges et aux naines blanches qui accusent des écarts importants avec la loi statistique .
Les variables à éclipse permettent de calculer le diamètre des étoiles
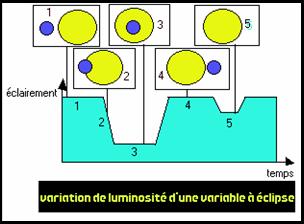
Ce qu'on appelle variable à éclipse , n'est pas autre chose qu'un couple de même nature que le précédent dont le plan orbital passe par la Terre . On voit l'orbite par la tranche .
Le compagnon étant plus petit et moins lumineux que l'étoile principale , il provoque une diminution de la luminosité totale quand il s'interpose entre elle et nous (2) avec un minimum très marqué quand il est tout entier contenu dans sa grande sœur (3).
Le maximum de luminosité est atteint lorsque les deux étoiles sont visibles sans se recouvrir (1 et 4) et on observe un second minimum , beaucoup moins marqué , quand la grande étoile cache entièrement la petite (5).
Connaissant la distance du couple à la Terre , il est facile de calculer le diamètre des étoiles à partir d'une courbe donnant la variation d'éclairement en fonction du temps.
Pour estimer le diamètre des étoiles , il existe d'autres méthodes moins fiables :
l Si l'étoile est assez grande on peut séparer ses bords extrêmes en deux sources qu'on fait interférer.
Mais les dimensions du plus grand diamètre apparent d'étoile (0,047" avec Mira Céti de la Baleine) montre les limites de cette méthode .
l Pour les grandes étoiles de l'écliptique (Antarès) on peut étudier leur occultation par la Lune .
La plus grande étoile connue est V.V Céphéi (2400 diamètres solaires) . Les naines blanches sont à peu prés grandes comme la Lune et les étoiles à neutrons auraient un diamètre d'environ 20 km (sous toute réserve) .
|
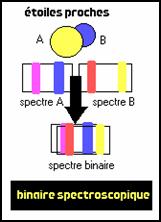
Les binaires spectroscopiques sont si rapprochées que même les instruments les plus puissants ne peuvent les séparer mais une étude du spectre lumineux révèle que certaines raies dérivent successivement vers le rouge puis vers le bleu .
Ce sont en réalité les raies du spectre du compagnon qui gravite autour de l'étoile principale dans une configuration semblable à celle des variables à éclipse , ce qui fait que ses raies, évoluent vers le rouge ou le bleu, conformément à l'effet Doppler - Fizeau, selon qu'il s'éloigne ou se rapproche de nous .
Cet effet est d'autant plus perceptible que la grande majorité des binaires spectroscopiques sont très proches l’une de l’autre, avec des périodes souvent inférieures à deux jours et ont des trajectoires à l'excentricité très marquée . Or une forte ellipticité est synonyme d'une trajectoire variant profondément en avant et en arrière et de fortes accélérations permettant d'atteindre des vitesses énormes .
L'étude de la variation du spectre confirme cette grande excentricité mais donne peu de renseignements annexes sur les orbites ou les masses .
Connaissant la masse et le diamètre , on peut calculer la masse volumique de certaines étoiles qui atteint
100 tonnes/cm3 pour les naines blanches et 10 milliards de tonnes /cm3 pour les étoiles à neutron contre
0,1 microgramme/cm3 pour une géante rouge .
Champ magnétique et vitesse de rotation
Pour finir d'illustrer la richesse des renseignements fournis par le spectre optique , il faut encore citer
l l'effet Zeeman qui permet de calculer le champ magnétique d'une étoile
l et le lien entre l'épaisseur des raies spectrales et la vitesse de rotation .
Zeeman a en effet démontré que sous l'effet d'un champ magnétique intense, une raie d'émission peut apparaître en triple exemplaire (dans le cas le plus simple), avec deux raies fantômes de part et d'autre de la raie théorique.
La mesure de l'amplitude du triplet permet de calculer le champ magnétique de l'étoile et fait apparaître , dans la centaine de cas où elle a été menée à bien , des valeurs très élevées (de l'ordre de la centaine de Gauss ou plus contre 0,5 pour le champ magnétique terrestre) .
Pour évaluer la vitesse de rotation des étoiles sur elles mêmes, on utilise la mesure de l'épaisseur des raies spectrales. Plus la rotation est rapide, plus l'élargissement est conséquent .
Ceci - dit , cet effet est maximal quand l'étoile nous présente son diamètre équatorial et nul si on en a une vue polaire . Et comme la distribution des vues est aléatoire , le chiffre mesuré ne donne qu'une indication moyenne .
On constate cependant que la vitesse de rotation moyenne varie avec la classe spectrale c'est à dire la composition de l'étoile . Elle peut atteindre 560 km/s pour les étoiles qualifiées de primitives (dépourvues de raies métalliques) alors que pour le soleil , elle n'est que de 2 km/s .
On pense que les étoiles primitives , à rotation rapide, sont aplaties et émettent même des jets de matière gazeuse dans leur plan équatorial , ce qui explique qu'on trouve dans leur spectre des raies d'émission en plus grand nombre .
Ajoutons que, si l'on excepte le cas particulier du soleil , pour lequel on utilise des techniques de substitution , il est impossible de déterminer les vitesses de rotation inférieures à 20 km/s car l'erreur commise est du même ordre que la mesure .