

Selon qu'on utilise le calendrier anglais de l'époque (calendrier julien) ou le calendrier grégorien , déjà en vigueur en France, Newton est né le 25 décembre 1642 (l'année de la mort de Galilée) ou le 4 janvier 1643.
Il accomplit ses études au collège de Grantham avant d'être envoyé à l'université de Cambridge à 18 ans.
En 1665 , poussé par la peste qui sévit à Londres , il revient chez lui , sa licence en poche, puis retourne à Cambridge en 1667 et obtient sa maîtrise l'année suivante avant d'y devenir professeur en 1669.
Au début de sa carrière, il travaille seul , négligeant les programmes universitaires, pour se consacrer à ses deux passions : les mathématiques et la physique .
En 1672 , il envoya à la Royal Sociéty un bref exposé de sa théorie des couleurs où il expliquait que la lumière est un mélange de différentes couleurs et que certains procédés comme la diffraction par un prisme ou la réflexion permettent d'en dissocier les composantes . Il fut publié mais mal accueilli par ses pairs.
Newton fut un farouche opposant au roi Jacques II qui voulait faire de Cambridge une institution catholique. Après la révolution de 1688, ses prises de position antérieures lui valurent d'être nommé directeur de l'université, puis président de la Monnaie Royale, puis président de la Royal Sociéty, par le nouveau régime .
L' ascension sociale de Newton coïncide avec la publication d'une oeuvre colossale mais chacune de ses communications fut entachée par de graves différends avec la communauté scientifique .
En 1663 James Gregory émet l'idée d'un télescope à réflecteur , en 1668 Newton en construit un et s'en attribue la paternité.
En 1684 , suite à une visite de Halley , il créa la dynamique en énonçant les règles fondamentales du mouvement et les appliqua aux résultats de Kepler pour formuler les lois de la gravitation universelle .
En 1687, il publia ses résultats dans « Philosophiae Naturalis Principia Mathematica » et fut aussitôt violemment pris à parti par Robert Hooke qui lui reprocha de lui avoir volé l'idée centrale à savoir que deux corps s'attirent avec une force qui diminue quand leur distance augmente.
Les historiens donnent plutôt raison à Newton dans cette querelle mais la véhémence de Hooke et la publication tardive de Newton justifient certains doutes .
En 1693 , Newton fut victime de puissants troubles émotifs dont il se rétablit mais qui mirent un terme à sa créativité .
En 1703 , alors qu'il venait d'être élu président de la Royal Sociéty , il ordonna la publication immédiate du résultat des observations de Flamsteed dont il avait besoin pour sa théorie de la lune . Il s'ensuivit un douloureux conflit avec l'astronome .
Il disputa à Leibnitz la paternité du calcul différentiel qu'il appelait "calcul des fluxions", (exposé pour la 1ere fois en appendice de Opticks en 1704 et maladroitement utilisé dans les Principia 1687) mais c'est son rival qui publia le premier (1684-1686) et fit adopter les notations actuelles de l'intégrale et de la différentielle .
Newton accusa Leibnitz de plagiat et nomma une commission d'enquête dont il rédigea lui même les conclusions. Selon Newton, il aurait confié en 1669 à Isaac Barrow son professeur de mathématiques, un manuscrit sur le sujet dont le titre est "De Analysis". Mais ce manuscrit n'ayant jamais été publié on ne voit pas comment Leibnitz aurait pu en avoir connaissance.
A l'heure de sa mort , en 1727, la controverse était encore chaude .
Si les scientifiques devaient jalonner l'histoire de la pensée universelle par les grands noms qui lui ont donné une impulsion décisive , probablement que Copernic et Newton occuperaient une place de choix alors que Kepler serait moins souvent cité . Pourtant si Copernic a formulé les grandes lignes du système révolutionnaire qui allait s'imposer aux générations futures , il n'était pas le premier .
Aristarque et Oresme l'avaient fait avant lui mais ils n'avaient pas été relayés par un Kepler pour donner à leur modèle sa simplicité féconde , sa formulation mathématique et surtout son caractère irréfutable devant les observations par l'introduction de l'ellipse qui est une révolution sans doute moins spectaculaire mais aussi probablement plus subtile , plus difficile et plus féconde que tous les résultats antérieurs .
Le système grec dont avait hérité Copernic n'était pas celui de l'obscur inconnu qui avait décidé de l'ordre des orbites planétaires , c'était celui de Ptolémée qui avait donné aux orbites une formulation mathématique permettant de prédire et de contrôler la position des planètes .
De la même façon , le système dont va hériter Newton , n'est pas celui de Copernic : c'est celui de Kepler. Et celui de Kepler contient déjà les germes de la gravitation universelle. C'est lui et non Copernic qui a débarrassé le système que les grecs nous avaient légué des épicycles et autres équants , ces anticorps destinés à leurrer notre perception de l'univers .
Voyons en quoi on peut estimer que Kepler et Galilée ont largement contribué à faire le lit de Newton :
C'est à cette époque que fut élaborée la notion de pesanteur avec des connotations diverses :
Copernic pensait que la pesanteur caractérisait la tendance des planètes à adopter une forme sphérique .
Galilée pensait que la pesanteur était inhérente à la matière terrestre et qu'elle influençait la matière céleste dans sa propension à se mouvoir en cercle mais cette propension caractérisait l'état d'inertie (aucune force)
Kepler fut le premier à émettre l'hypothèse que la pesanteur découlait de l'attraction mutuelle de deux corps et que, si ceux - ci n'étaient soumis à aucune autre influence, ils se précipiteraient l'un vers l'autre, en accomplissant des distances inversement proportionnelles à leur masse .
Kepler avait aussi postulé que les marées étaient dues à l'influence gravitationnelle de la lune avant de reculer et d'abandonner la pesanteur au profit d'une théorie magnétique .
|
|
Quant à Galilée , ses travaux restaient en général confinés au plancher des vaches, mais il posa les fondements de la dynamique et étudia la chute des corps .
Par exemple , il avança qu'on peut dissocier la chute de l'un des projectiles de la figure 1 en deux mouvements .
L'un est horizontal et dépend de la vitesse d'impulsion v .
Si le projectile met un temps t à atteindre le point A , la distance DA est égale à v.t . Tout se passe comme si horizontalement , le mouvement se poursuivait à vitesse constante .
Le mouvement vertical , quant à lui , (mesuré par y=½ gt2) ne se déroule pas à vitesse constante . Il est accéléré et analogue à celui qu'on obtiendrait si on laissait tomber le projectile sans vitesse initiale.
Cette décomposition de la chute est l'amorce du raisonnement qui permettra à Newton de découvrir la gravitation universelle. Le mouvement horizontal est uniforme et dû à l'impulsion initiale qui confère au projectile la vitesse v. Si le projectile n'était pas soumis à la force de pesanteur, qui l'attire vers le sol et va limiter la durée de la trajectoire à l'impact avec sa surface , en A , le mouvement se poursuivrait indéfiniment selon la direction horizontale en conservant la même vitesse .
C'est d'ailleurs ce qu'exprima Descartes un peu plus tard et qui fut repris par Hooke , puis Newton dans sa première loi :
Un corps soumis à aucune force est soit immobile , soit animé d'un mouvement rectiligne uniforme (c'est à dire se déroulant en ligne droite et à vitesse constante) . Si sa trajectoire n'est pas rectiligne ou sa vitesse inconstante, c'est qu'il est soumis à l'influence d'une force . Galilée n'était pas allé jusque là et admettait qu'en l'absence de force , à l'échelle astronomique, un point pouvait décrire un cercle .
Pour expliquer la façon dont se meuvent les planètes, Kepler ou Descartes avaient supposé que le soleil pouvait exercer sur elles une force semblable à celle qui attire les corps vers le sol mais ils avaient négligé l'hypothèse d'une impulsion initiale . Si bien qu'on avait une corde qui tenait la planète attachée au soleil , mais il fallait y ajouter un moteur pour lui conférer un mouvement de rotation . Pour Kepler , c'était l'anima motrix, pour Descartes c'était un tourbillon de l'éther céleste.
En 1674 , (c'est à dire 13 ans avant que Newton ne publie ses travaux et 8 ans après qu'il ait prétendu avoir obtenu des résultats équivalents) Hooke énonce clairement 3 lois
1) Tous les corps s'attirent mutuellement par gravitation
Cette force s'exerce de centre à centre . Elle est responsable à la fois de la cohésion des astres autour de leur centre et de l'attraction des astres entre eux .
2) Tous les corps qui ont reçu une impulsion se meuvent en ligne droite jusqu'à ce qu'une force s'exerce sur eux et les oblige à décrire un cercle , une ellipse ou quelque autre courbe compliquée .
3) La force attractive est d'autant plus forte que les corps sont plus proches de centre à centre mais j'ignore dans quelle proportion .
Si bien que tous les éléments qui devaient conduire à la gravitation universelle étaient dans l'air , 40 ans après la mort de Galilée mais il fallait un Newton pour en faire la synthèse et l'exprimer sous une forme mathématique . D'ailleurs suivons son raisonnement dans Le Système du Monde
|
|
Reprenant le projectile de Galilée , il en hisse l'élément moteur sur une montagne et lui donne des impulsions de plus en plus grandes qui lui font toucher le sol de plus en plus loin : 1,2,3,4 ...
Il doit exister une vitesse critique Vc donnant au projectile la trajectoire 5 qui le voit revenir à son point de départ . Et si, conformément aux résultats de Galilée, la composante horizontale du mouvement (traduisez tangentielle) est constante, il y revient avec une vitesse Vc, celle qu'il avaitinitialement , ce qui va lui permettre d'amorcer une nouvelle révolution semblable à la première . On obtient ainsi une nouvelle lune , un "satellite" pour reprendre le terme inventé par Kepler.
Il suffit de calibrer convenablement l'impulsion initiale et la hauteur de la montagne pour justifier toutes les trajectoires planétaires .
On voit donc que le bouillonnement des esprits initié par Kepler et Galilée mettait la découverte de la gravitation universelle à la portée d'un faible saut théorique , sans aucune commune mesure avec celui qu'avaient effectué les précurseurs immédiats et que la pomme de Newton n'était pas porteuse d'autant de nouveautés que le laissent penser la plupart de ses hagiographes .
Mais il fallait maintenant mettre tout cela en équations et prouver que les travaux de Kepler s'accordaient avec les formules obtenues . Dans ce chapitre , Newton s'avéra excellent mais là encore , on va voir que les procédés qu'il utilisa dans ses calculs ne recelaient aucune réelle nouveauté .
Les principes du calcul différentiel avaient été publiés par Leibnitz en 1675 et l'idée forte de ce procédé qui consistait à postuler que la plupart des valeurs (comme la vitesse) étaient constantes sur un très faible intervalle de temps avait déjà été tutoyée par Kepler dans la loi des aires, Neper ou Cavalieri . .
Quant à la décomposition des mouvements en effets radial (gravitation) et tangentiel (impulsion) , c'était la transposition aux trajectoires fermées des résultats de Galilée sur les trajectoires ouvertes (et décomposées en effets vertical et horizontal).
Dans le livre I , Newton donne les définitions et principes qui fondent sa dynamique et en déduit les lois du mouvement.
Certains principes sont empruntés à ses prédécesseurs (notamment Descartes) :
l en l'absence de force extérieure, la matière est soit immobile, soit animée d'un mouvement rectiligne uniforme.
l toute dérogation à ce principe est le signe que s'exerce une force extérieure .
D'autres plus novateurs permettent de décrire et quantifier l'action des forces extérieures. Ils précisent aussi l'idée de pesanteur :
l les changements qui arrivent dans le mouvement sont proportionnels à la force motrice et se font dans la direction où elle s'exerce .
l l'action est égale à la réaction , c'est à dire que les forces exercées par le corps A sur le corps B sont égales aux forces exercées par le corps B sur le corps A .
l la quantité de mouvement est le produit de la masse par la vitesse .
l la quantité motrice de la force accélératrice est proportionnelle au mouvement produit en un temps donné .
Enfin , les principes et les lois qui s'appliquent plus précisément aux mouvements circulaires ont été défrichés par Huygens dés 1658 mais Newton les expose différemment , en donne une formulation plus fertile pour la mécanique (on peut les étendre aux mouvements elliptiques) , et surtout , il fait le lien entre la pesanteur et la production de ces trajectoires (ce à quoi Huygens n'a pas pensé) :
l la force centripète est celle qui fait tendre un corps vers un point , comme vers un centre .
l la quantité absolue de force centripète est fonction de la cause qui la propage au centre .
l la quantité accélératrice de la force centripète est proportionnelle à la vitesse produite en un temps donné .
Reste à déduire de ces hypothèses les résultats quantitatifs qui les confirment .
Ici , on met forcément le doigt sur le degré de filiation entre les lois de Kepler et celles de Newton .
Newton doit en effet démontrer que ses lois confirment celles de Kepler , à savoir …
1) que la trajectoire imposée par l'interaction de deux corps pesants dont l'un est initialement animé d'un mouvement rectiligne doit être une ellipse ou un cercle .
2) que le mouvement ainsi produit doit vérifier la loi des aires (les aires balayées par les rayons orbitaux dans des temps égaux doivent être égales) et la 3eme loi (le rapport du cube du rayon de l'orbite au carré de la période doit être constant) .
Inversement , il est évident que les lois de Képler sont riches d'inférences susceptibles de mettre Newton sur la voie de ses propres découvertes .
Ce n'est pas pour rien que les premières propositions véritablement quantitatives énoncées par Newton concernent la loi des aires . Elles postulent qu'un corps initialement en mouvement rectiligne soumis à une force centrale épouse une trajectoire vérifiant la loi des aires et qu'inversement , si la trajectoire d'un corps vérifie la loi des aires , c'est qu'il est soumis à l'action d'une force centrale .
Suivons sa démonstration de la proposition directe :
|
|
Figure 1 :
Le corps suit un mouvement rectiligne de A à C en parcourant une distance d pendant un temps t .
En C, il subit l'action d'une force centrale dirigée de C vers O pendant un temps t.
Sans cette force , il serait parvenu en D' tel que CD'=d .
Sans vitesse initiale il aurait parcouru la distance CC' .
En combinant les deux , il a parcouru la distance CD diagonale du parallélogramme CD'DC' .
Si on pose H=OH et h=Oh , pendant le trajet rectiligne , la loi des aires est respectée : l'aire des triangles jaune et vert est d.H/2 . L'aire du triangle bleu est égale à aire(OC'D)+aire(CC'D) soit d.h/2 + d.(H-h)/2 soit encore d.H/2 .
Le mouvement provoqué par une force centrale vérifie la loi des aires .
Remarquons que la décomposition des mouvements en deux axes s'inspire du procédé utilisé pour la parabole de Galilée .
La distance CC' = DD' , due au travail de la force centrale, que Newton appelle "force centripète" est qualifiée "d'écart à la loi d'inertie" . En effet , D' est bien le point où se situerait le mobile au bout d'un temps Dt s'il n'était soumis à aucune force (loi d'inertie) et D est le point où il se trouve au bout du même délai quand il est soumis à l'action de la force centripète .
L'une des propositions de Newton affirme que tout se passe comme si la force centripète produisait une vitesse radiale (selon CC') dont la variation en un temps donné est proportionnelle à ce qu'il appelle la quantité accélératrice de la force . (On dirait aujourd'hui l'accélération A). Cette proposition est elle vraiment novatrice ?
Dans l'expérience de Galilée , si on lâche une bille depuis une certaine hauteur sans vitesse initiale au temps zéro la distance qu'elle aura parcouru vers le sol au temps t sera l = ½ At2 (avec A = g) et la vitesse atteinte au même instant sera V=At (en dérivant V=dl/dt) .
Cela veut dire qu'en 1 seconde , la vitesse augmente de A , en 2 secondes , elle augmente de 2A , etc ..
La variation de vitesse en un temps donné est donc proportionnelle à l'accélération A .
Les résultats de Galilée contiennent donc déjà la proposition de Newton . La nouveauté consiste simplement à comprendre que la force centrale qui attire une planète vers le soleil est de même nature que celle qui attire la bille vers le sol et d'en déduire que quantitativement , les mouvements qui en résultent obéissent aux mêmes lois.
La véritable innovation apparaît sous la forme anodine de la définition de la quantité de mouvement q=mV .
On pourrait penser que cette définition vient comme un cheveu sur la soupe , si deux propositions ultérieures ne venaient lui donner un éclairage singulier :
l les changements qui arrivent dans le mouvement sont proportionnels à la force motrice et se font dans la direction dans laquelle la force a été imprimée .
l la quantité motrice de la force accélératrice est proportionnelle au mouvement qu'elle produit en un temps donné .
Que faut - il entendre par là ?
Si , par "mouvement" on entend "quantité de mouvement", et si , dans l'expérience de Galilée, m est la masse de la bille, V=at sa vitesse à l'instant t, « les changements qui arrivent dans le mouvement » (c’est à dire la variation de sa quantité de mouvement) entre 2 instants t1 et t2 est
mAt2 - mAt1 soit mA(t2 - t1) .
En somme cette variation est mA en 1 seconde , 2mA en 2 secondes , etc ...
Les deux propositions de Newton reviennent à affirmer que si F est la force imprimée : F=KmA .
On retrouve donc pratiquement l'actuelle formule fondamentale de la dynamique F=mA pourvu qu'on exprime F , m et A en des unité cohérentes . Mais l'unité de force qui permet de s'affranchir du coefficient de proportionnalité K n'a pas encore été inventée : elle va s'appeler le Newton .
On peut donc en déduire que si Newton a introduit la notion de quantité de mouvement , c'est qu'il avait eu l'intuition géniale de la proportionnalité de la force aux masses en mouvement et à l'accélération produite .
C'est surtout en cela que ses travaux étaient extrêmement novateurs .
Reste, maintenant à déterminer la forme de l'accélération A. Si elle est constante (et égale à g) dans l'expérience de Galilée , il doit en aller de même pour les planètes puisque le fait que celles ci se meuvent sur des trajectoires assimilables à des cercles , semble suggérer que la force qui s'exerce sur chacune d'elles est constante .
Il est , en effet , assez logique de penser que si la force variait grandement , la planète se rapprocherait ou s'éloignerait très sensiblement du soleil et la périodicité de sa trajectoire serait menacée.
Parmi tous les mouvements qui vérifient la loi des aires , le plus simple et le plus pur est le mouvement circulaire uniforme qui voit un mobile parcourir un cercle à vitesse linéaire V (ou vitesse angulaire w ) constante .
D'après ce qui précède , ce mouvement doit être produit par une force centrale constante et donc une quantité accélératrice constante . Il devrait être idéal pour étudier la forme de cette grandeur .
|
|
Figure 2 :
Si la vitesse en T est V (supportée par la tangente au cercle de rayon r) :
sans accélération centrale , le mobile aurait parcouru la distance TP= V.Dt au bout d'un temps Dt .
L'accélération centrale, le ramenant vers O, lui a fait parcourir l'arc TM= V.Dt.
PM = e est l'écart à la loi d'inertie , correspondant au travail de la force centrale (l'équivalent du segment DD' de la figure 1) .
La constance de la puissance du point P par rapport au cercle exprime que
PM.PR=PT2. Ou bien 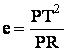 .
.
Si la direction PM ne passe pas par O , c'est tout simplement que le temps Dt choisi n'est pas assez petit . Plus Dt tend vers un temps dt très petit , plus la droite PR se rapproche du point O et la grandeur PR se rapproche du diamètre du cercle (2r)
On peut alors écrire que PT=v.dt et e = 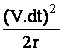
Pendant un temps très court (dt) , on peut donc considérer que la proposition de Newton qui énonce que "les changements qui arrivent dans le mouvement sont proportionnels à la force motrice et se font dans la direction dans laquelle cette force a été imprimée " est vérifiée . Il suffit de recommencer l'opération en M un grand nombre de fois pour parcourir le cercle en entier à base de petits arcs successifs .
A ce stade , on pourrait se contenter d'assimiler e à une distance résultant d'un mouvement galiléen e= ½ A(dt)2, pour éliminer le temps dans l'expression précédente et trouver
A=K![]() , formule que Huygens a établi depuis 1658 .
, formule que Huygens a établi depuis 1658 .
On peut aussi dire que pour t très petit e = ![]() .
.
En calculant la dérivée on trouve que e grandit à la vitesse ![]() . En une seconde , cette vitesse croît de
. En une seconde , cette vitesse croît de ![]() .
.
Ce qui établit la proportionnalité de A à ![]() d'après les propositions de Newton .
d'après les propositions de Newton .
A ce stade , il est temps de faire intervenir la 3eme loi de Kepler , comme l'a fait Newton :
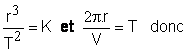 rV² = constante = k'
rV² = constante = k'
En reportant ce résultat dans 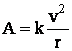 il vient
il vient ![]() .L'accélération résultant d'une force centrale est en 1/r2 .
.L'accélération résultant d'une force centrale est en 1/r2 .
En réalité , il y a plusieurs failles dans la démarche exposée dans les Principia :
1) D'après certains auteurs , la démonstration de Newton ferait la part belle aux deux dernières lois de Kepler mais il se serait racheté dans un manuscrit préparatoire , où il aurait dit : "les forces centripètes des corps qui se meuvent uniformément sur des circonférences de cercles sont comme les carrés des arcs décrits dans un même temps" . Or, n'en déplaise au biographe, cette proposition , qui n'est vraie que pour des mouvements uniformes se déroulant à vitesses différentes sur des cercles de même rayon n'est pas du tout équivalente à une proportionnalité de l'accélération à V2/r
2) Comme le démontrera un peu plus tard Newton lui même , la troisième loi de Kepler n'est juste que si les planètes pèsent la même masse ou si elles décrivent des cercles parfaits . Ce n'est manifestement pas le cas .
3) Les lois de Kepler sont des lois expérimentales (résultats d'une observation) et la rigueur imposait qu'on les déduisit des résultats de Newton et non pas le contraire .
Mais ne chicanons pas trop notre homme qui se rattrapera dans le livre III des Principia en démontrant brillamment qu'il suffit de postuler que la force exercée entre le soleil et les planètes est de la forme K/r2 pour que leurs trajectoires soient des ellipses , pour que la loi des aires soit vérifiée, ainsi que la 3eme loi de Kepler modifiée et précisée sous la forme
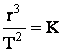 (m+M) où K est une constante, m la masse de la planète, et M celle du soleil .
(m+M) où K est une constante, m la masse de la planète, et M celle du soleil .
Il suffit de réaliser que pour toutes les planètes m est plus de 1000 fois plus petit que M pour comprendre que la quantité K(m+M) est très voisine de KM et donc pratiquement constante .
Dans le livre III , Newton précisera aussi la forme de la force de gravitation .
Dans le livre I , on a appris qu'elle était de la forme F=kmA ou F=Km/r2 où m est la masse de la planète et r la distance entre le soleil et la planète .
Mais le principe de l'action et de la réaction postule que la force exercée par le soleil sur la planète est égale à la force exercée par la planète sur le soleil qui, elle, est de la forme KM/r2. Cette force a donc l'obligation d'être à la fois proportionnelle à m et M ce qui donne la formule définitive : 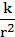
Enfin , toujours dans le livre III des Principia, Newton démontrera que les trajectoires des comètes obéissent aussi à la gravitation universelle et décrivent soit des ellipses excentriques (aplaties) , soit des paraboles .
Des lois de Newton à l'ellipse.
Newton a démontré
a) qu'un mobile ayant une vitesse initiale et soumis a une force centrale respecte la loi des aires
b) que l'accélération du mouvement est de la forme ![]() , k étant une constante et r la distance du mobile au soleil.
, k étant une constante et r la distance du mobile au soleil.
Par ailleurs comme Newton nous maîtrisons les rudiments du calcul différentiel et nous savons un certain nombre de choses sur l'ellipse.
(Synthèse dans la figure ci contre).
Parmi toutes nos connaissances sur l'ellipse, la plus utile sera certainement celle qui définit le rayon vecteur r joignant un foyer à un point M de la figure dont la mesure est donnée par la formule
r = ![]()
où ρ et e sont des constantes et ɵ l'angle que fait le rayon vecteur avec le grand axe.
Donc, en gros, pour démontrer que la trajectoire d'un corps soumis aux forces de Newton est une ellipse, il faut démontrer
que ![]() est de la forme k – k'cos(ɵ). Puis vérifier que k et k' sont compatibles avec le ρ et le e d'une ellipse, notamment e<1.
est de la forme k – k'cos(ɵ). Puis vérifier que k et k' sont compatibles avec le ρ et le e d'une ellipse, notamment e<1.
Nous nous bornerons à démontrer que ce résultat est assez simple à établir à partir de ce que sait Newton, sans pour autant suivre le cheminement du savant que le langage de son temps rend difficile à déchiffrer.
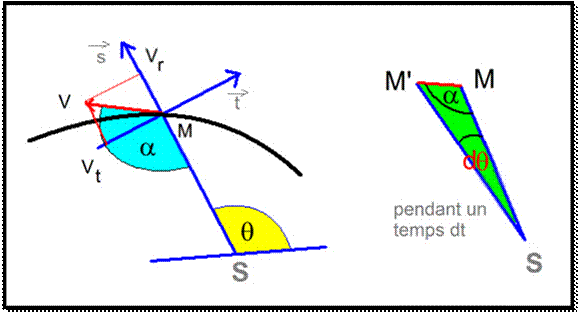
Sur le dessin de gauche, S est le soleil, M le corps mobile, ɵ est l'angle que fait SM avec une droite fixe arbitraire passant par M.
α est l'angle que fait la vitesse du mobile avec SM.
Nous avons décomposé la vitesse en Vr et Vt, ses composantes selon 2 axes perpendiculaires de vecteurs unitaires ![]() (colinéaire à
(colinéaire à ![]() ) et
) et ![]() .
.
Le dessin de droite montre l'évolution du mobile pendant un temps dt très court.
On a ![]() =Vr
=Vr![]() +Vt.
+Vt.![]() =
= ![]()
a) utilisation de la loi des aires.
Dans le dessin de droite, MM' = Vdt . La surface du triangle SMM' est MM'.SM.sin(α) = V.r.sin(α).dt et cette quantité étant constante pour un temps dt, V.r.sin(α)= K est constant.
Or V. sin(α) est Vt, composante de la vitesse selon ![]() , ce qui donne
, ce qui donne ![]() . ou
. ou ![]() ou
ou ![]() résultats importants qui vont nous permettre d'éliminer le temps des équations.
résultats importants qui vont nous permettre d'éliminer le temps des équations.
b) utilisation d'une accélération en ![]() .
.
Si on dérive la vitesse par rapport au temps, on trouve l'accélération.
![]() =[
=[![]() + [2
+ [2![]() .
.
Or la composante en ![]() de l'accélération est égale à
de l'accélération est égale à ![]() , cette quantité étant nulle en tant que dérivée d'une constante.
, cette quantité étant nulle en tant que dérivée d'une constante.
On en déduit que a = ![]() avec
avec ![]() =r
=r![]()
Par ailleurs
![]()
et donc
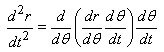
=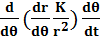 =
= 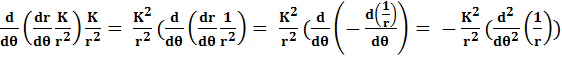
si nous regroupons tous les termes:
a = 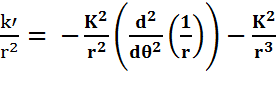
et après simplification
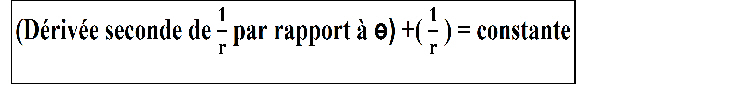
Equation différentielle dont l'ellipse en notation polaire 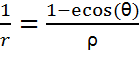 est une solution puisque la dérivée seconde de
est une solution puisque la dérivée seconde de ![]() est
est 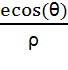 .
.
Une question intéressante est de savoir ce qui détermine la forme d'une l'orbite, quand la gravitation se manifeste, lors d'une captation.
Outre les masses respectives des 2 objets, 3 paramètres jouent un rôle : la valeur de la vitesse initiale , sa direction et la distance à la masse attractive. En gros :l plus on rapproche l'objet capté, plus on le dirige vers la masse attractive, plus on diminue sa vitesse, plus on favorise la collision.
l Entre évasion et collision , l'objet décrit des trajectoires fermées plus ou moins elliptiques dont le cercle correspond à une situation intermédiaire qui va voir changer la direction du grand axe .
Il suffit donc de donner la masse des 2 objets, leur distance et le vecteur vitesse de celui qui est supposé mobile et va être capté, pour calculer la trajectoire qu'il va adopter .
C'est ainsi qu'on procède , avec les engins spatiaux, qu'on peut poser sur une planète , satelliser ou balader dans tout le système solaire avant qu'ils ne s'en évadent en une trajectoire hyperbolique .
Il faut d'abord leur donner une vitesse d'évasion (qui est de l'ordre de 11km/s à 200km de hauteur) afin qu'ils échappent à la force de gravitation terrestre (c'est le rôle du lanceur qui fournit le gros du travail) , puis leurs propres moteurs , orientables, permettent de leur donner des impulsions qui vont permettre de choisir ou de corriger leurs trajectoires avec des dépenses d'énergie d'autant plus modestes qu'ils se tiennent éloignés des planètes ou autres objets attractifs. C'est en expulsant du gaz à grande vitesse que le moteur agit . Le principe est le suivant : si M est la masse du satellite , l'éjection d'une masse m de gaz à une vitesse v confère au satellite une vitesse V opposée à v et respectant la formule MV=mv .
La trajectoire elliptique s'explique comme un conflit entre la gravité (force centripète) et la force centrifuge.
|
|
Prés du périgée (de S à P) , la Terre incurve la trajectoire de la lune pour tenter de la capter , mais cela augmente la force centrifuge . Imaginez que durant une course rectiligne vous attrapiez un poteau : vous allez obligatoirement tourner autour de lui et la force que vous allez exercer pour ne pas le lâcher sert à compenser la force centrifuge . Dans ce mouvement la lune (qui a happé le poteau terre), a pris de la vitesse et elle est éjectée en direction de S' .
A partir de là , tout se passe comme quand on lance un cailloux vers le ciel . Sous l'action des forces de gravité son énergie cinétique (½mV²) , sa vitesse, diminue et son énergie potentielle (mAr) augmente.
Rappelons que , les masses s'attirant entre elles , pour leur donner de l'énergie potentielle, il suffit de les écarter.
En l’absence de frottements, quand on les lâchera , la force de gravité jouera le rôle d'un élastique et les rapprochera , produisant un travail .
Remarquons au passage que dans un mouvement circulaire uniforme, V et r sont constants , A=V²/r si bien que l'énergie potentielle est égale à mV² et les deux énergies restent constantes .
A l'apogée (A), la gravité prend le pas sur la force centrifuge et c'est le rappel, comme si la lune retombait sur la terre en s'accélérant .L'énergie cinétique prend le pas sur l'énergie potentielle et quand la lune retrouve son point de départ, le bilan énergétique est identique à sa valeur initiale (en S) .
La lune retrouve les conditions qui lui ont fait faire un tour de la terre : elle va en entreprendre un autre .
Voilà donc quels sont les principaux résultats du livre III des Principia . Pour ce qui concerne le livre II , disons seulement qu'il traite des modifications que subissent les mouvements quand ils se produisent dans un milieu fluide et résistant . Un cas de figure présentant très peu d'intérêt pour l'astronomie .
Le caractère magique des travaux de Newton tient à l'explication de toute la mécanique astrale à partir d'une hypothèse ultra simple : la forme mathématique de la force exercée .
Et cette découverte dépasse largement les cadres de l'astronomie et de la gravitation . Elle trouve une foule d'applications dans la vie pratique et les théories scientifiques où de nombreuses forces sont de même nature que celles qu'a étudié Newton .
Il n'est pas anormal que l'homme qui semble avoir plié l'univers à ses lois, jouisse, aux yeux de l'humanité d'un statut de géant , mais nous , nous savons tout ce que lui ont apporté les petites fourmis laborieuses qui l'ont précédé , les Copernic , Galilée , Kepler , Descartes sans qui Newton aurait hérité d'un marais théorique fangeux au lieu de la voie royale qui l'a mené au succès .D'ailleurs, sans diminuer son mérite, toutes les controverses de Newton avec ses rivaux moins prestigieux (Leibnitz , Hooke, Huygens, Flamsteed,...) ne prouvent-elles pas, à l'évidence, que sa pomme était mûre longtemps avant sa chute.
Si nous mettons tant de bémols à la partition de Newton , c'est moins pour déprécier son oeuvre que pour ramener le génie à de plus justes proportions . En creusant un peu , on trouve toujours dans la généalogie d'un génie , une longue lignée de tâcherons plus ou moins anonymes qui à force de violer consciencieusement la science finissent par donner le jour à un illustre bâtard . C'est comme si l'humanité toute entière , depuis la nuit des temps , travaille à son insu à ce feu d'artifice qui illuminera le savoir , on ne sait trop ni où ni quand .
Si l'anecdote de la pomme est vraie , qui dira assez le mérite de celui qui planta le pommier .
D'ailleurs , Newton est l'un des nombreux pères d'Einstein.
Mais il ne le sait pas encore .